
(学生活动)用配方法解下列方程
(1)6x2-7x+1=0 (2)4x2-3x=52
(老师点评) (1)移项,得:6x2-7x=-1
二次项系数化为1,得:x2-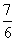 x=-
x=-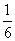
配方,得:x2-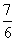 x+(
x+(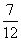 )2=-
)2=-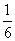 +(
+(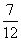 )2
)2
(x-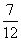 )2=
)2=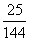
x-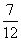 =±
=±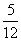 x1=
x1=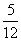 +
+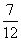 =
=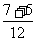 =1
=1
x2=-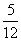 +
+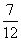 =
=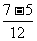 =
=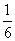
(2)略
总结用配方法解一元二次方程的步骤(学生总结,老师点评).
(1)移项;
(2)化二次项系数为1;
(3)方程两边都加上一次项系数的一半的平方;
(4)原方程变形为(x+m)2=n的形式;
(5)如果右边是非负数,就可以直接开平方求出方程的解,如果右边是负数,则一元二次方程无解.
5. 当k=0时, y=-2
当k=-1时,y1=-2,
y2=2.

2. x1=-b,x2=-b+2a
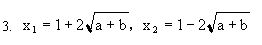
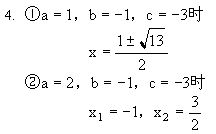
1. x1=a,x2=b
6. 解关于x的方程:(2x2-3x-2)a2 +(1-x2 )b2 -ab(1+x2 )=0
课堂练习(三)答案
5. 已知:关于y的一元二次方程(ky+1)(y-k)=k-2的各项系数之和等于3,求k的值以及方程的解.
3. 解关于x的方程x2 -4(a+b)+1=2x (a+b>0)
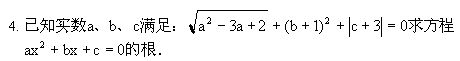
2. 解关于x的方程x2 -2(a-b)x+b2 =2ab
1. 解关于x的方程(x-a)2 +(x-b)2 =(a-b)2
9. 0
课堂练习(三)
解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com