
本节课要掌握:
(1)用因式分解法,即用提取公因式法、十字相乘法等解一元二次方程及其应用.
(2)三种方法(配方法、公式法、因式分解法)的联系与区别:
联系①降次,即它的解题的基本思想是:将二次方程化为一次方程,即降次.
②公式法是由配方法推导而得到.
③配方法、公式法适用于所有一元二次方程,因式分解法适用于某些一元二次方程.
区别:①配方法要先配方,再开方求根.
②公式法直接利用公式求根.
③因式分解法要使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0.
例3.我们知道x2-(a+b)x+ab=(x-a)(x-b),那么x2-(a+b)x+ab=0就可转化为(x-a)(x-b)=0,请你用上面的方法解下列方程.
(1)x2-3x-4=0 (2)x2-7x+6=0 (3)x2+4x-5=0
分析:二次三项式x2-(a+b)x+ab的最大特点是x2项是由x·x而成,常数项ab是由-a·(-b)而成的,而一次项是由-a·x+(-b·x)交叉相乘而成的.根据上面的分析,我们可以对上面的三题分解因式.
解(1)∵x2-3x-4=(x-4)(x+1)
∴(x-4)(x+1)=0
∴x-4=0或x+1=0
∴x1=4,x2=-1
(2)∵x2-7x+6=(x-6)(x-1)
∴(x-6)(x-1)=0
∴x-6=0或x-1=0
∴x1=6,x2=1
(3)∵x2+4x-5=(x+5)(x-1)
∴(x+5)(x-1)=0
∴x+5=0或x-1=0
∴x1=-5,x2=1
上面这种方法,我们把它称为十字相乘法.
教材P45 练习1、2.
(学生活动)请同学们口答下面各题.
(老师提问)(1)上面两个方程中有没有常数项?
(2)等式左边的各项有没有共同因式?
(学生先答,老师解答)上面两个方程中都没有常数项;左边都可以因式分解:
2x2+x=x(2x+1),3x2+6x=3x(x+2)
因此,上面两个方程都可以写成:
(1)x(2x+1)=0 (2)3x(x+2)=0
因为两个因式乘积要等于0,至少其中一个因式要等于0,也就是(1)x=0或2x+1=0,所以x1=0,x2=-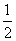 .
.
(2)3x=0或x+2=0,所以x1=0,x2=-2.
因此,我们可以发现,上述两个方程中,其解法都不是用开平方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次,这种解法叫做因式分解法.
例1.解方程
(1)4x2=11x (2)(x-2)2=2x-4
分析:(1)移项提取公因式x;(2)等号右侧移项到左侧得-2x+4提取-2因式,即-2(x-2),再提取公因式x-2,便可达到分解因式;一边为两个一次式的乘积,另一边为0的形式
解:(1)移项,得:4x2-11x=0
因式分解,得:x(4x-11)=0
于是,得:x=0或4x-11=0
x1=0,x2=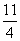
(2)移项,得(x-2)2-2x+4=0
(x-2)2-2(x-2)=0
因式分解,得:(x-2)(x-2-2)=0
整理,得:(x-2)(x-4)=0
于是,得x-2=0或x-4=0
x1=2,x2=4
例2.已知9a2-4b2=0,求代数式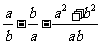 的值.
的值.
分析:要求 的值,首先要对它进行化简,然后从已知条件入手,求出a与b的关系后代入,但也可以直接代入,因计算量比较大,比较容易发生错误.
的值,首先要对它进行化简,然后从已知条件入手,求出a与b的关系后代入,但也可以直接代入,因计算量比较大,比较容易发生错误.
解:原式=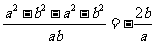
∵9a2-4b2=0
∴(3a+2b)(3a-2b)=0
3a+2b=0或3a-2b=0,
a=-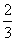 b或a=
b或a=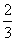 b
b
当a=-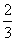 b时,原式=-
b时,原式=-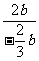 =3
=3
当a=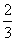 b时,原式=-3.
b时,原式=-3.
(学生活动)解下列方程.
(1)2x2+x=0(用配方法) (2)3x2+6x=0(用公式法)
老师点评:(1)配方法将方程两边同除以2后,x前面的系数应为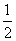 ,
,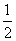 的一半应为
的一半应为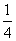 ,因此,应加上(
,因此,应加上(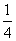 )2,同时减去(
)2,同时减去(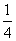 )2.(2)直接用公式求解.
)2.(2)直接用公式求解.
3.某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时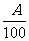 元收费.
元收费.
(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)
(2)下表是这户居民3月、4月的用电情况和交费情况
|
月份 |
用电量(千瓦时) |
交电费总金额(元) |
|
3 |
80 |
25 |
|
4 |
45 |
10 |
根据上表数据,求电厂规定的A值为多少?
2.设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,(1)试推导x1+x2=-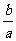 ,x1·x2=
,x1·x2=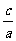 ;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
1.用公式法解关于x的方程:x2-2ax-b2+a2=0.
3.若关于x的一元二次方程(m-1)x2+x+m2+2m-3=0有一根为0,则m的值是_____.
2.当x=______时,代数式x2-8x+12的值是-4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com