例3．如图，在Rt△ACB中，∠C=90°，AC=8m，CB=6m，点P、Q同时由A，B两点出发分别沿AC、BC方向向点C匀速移动，它们的速度都是1m/s，几秒后△PCQ的面积为Rt△ACB面积的一半．

　　 分析：设x秒后△PCQ的面积为Rt△ABC面积的一半，△PCQ也是直角三角形．根据已知列出等式．

　　 解：设x秒后△PCQ的面积为Rt△ACB面积的一半．

　　 根据题意，得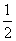：(8-x)(6-x)=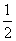××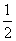8×6

　　 整理，得：x²-14x+24=0

　　 (x-7)²=25即x₁=12，x₂=2

　　 x₁=12，x₂=2都是原方程的根，但x₁=12不合题意，舍去．

　　 所以2秒后△PCQ的面积为Rt△ACB面积的一半．

　　 教材P₃₈　 讨论改为课堂练习，并说明理由．

　　 教材P₃₉　 练习1　 2．(1)、(2)．

　　 列出下面二个问题的方程并回答：

　　 (1)列出的经化简为一般形式的方程与刚才解题的方程有什么不同呢？

　　 (2)能否直接用上面三个方程的解法呢？

　　 问题1：印度古算中有这样一首诗：“一群猴子分两队，高高兴兴在游戏，八分之一再平方，蹦蹦跳跳树林里；其余十二叽喳喳，伶俐活泼又调皮，告我总数共多少，两队猴子在一起”．

　　 大意是说：一群猴子分成两队，一队猴子数是猴子总数的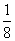的平方，另一队猴子数是12，那么猴子总数是多少？你能解决这个问题吗？

问题2：如图，在宽为20m，长为32m的矩形地面上，修筑同样宽的两条平行且与另一条相互垂直的道路，余下的六个相同的部分作为耕地，要使得耕地的面积为5000m²，道路的宽为多少？

　　 老师点评：问题1：设总共有x只猴子，根据题意，得：

　　　　　　　　 x=(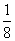x)²+12

　　 整理得：x²-64x+768=0

　　 问题2：设道路的宽为x，则可列方程：(20-x)(32-2x)=500

　　 整理，得：x²-36x+70=0

　　 (1)列出的经化简为一般形式的方程与前面讲的三道题不同之处是：前三个左边是含有x的完全平方式而后二个不具有．

　　 (2)不能．

　　 既然不能直接降次解方程，那么，我们就应该设法把它转化为可直接降次解方程的方程，下面，我们就来讲如何转化：

　　 x²-64x+768=0　 移项→ x=2-64x=-768

两边加(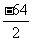)²使左边配成x²+2bx+b²的形式 → x²-64x+32²=-768+1024

左边写成平方形式 → (x-32)²=256 降次→x-32=±16 即 x-32=16或x-32=-16　

解一次方程→x₁=48，x₂=16

　　 可以验证：x₁=48，x₂=16都是方程的根，所以共有16只或48只猴子．

　　 学生活动：

　 　例1．按以上的方程完成x²-36x+70=0的解题．

　　 老师点评：x²-36x=-70，x²-36x+18²=-70+324，(x-18)²=254，x-18=±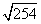，x-18=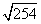或x-18=-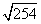，x₁≈34，x₂≈2．

　　 可以验证x₁≈34，x₂≈2都是原方程的根，但x≈34不合题意，所以道路的宽应为2．

　　 例2．解下列关于x的方程

　　 (1)x²+2x-35=0　　 (2)2x²-4x-1=0

　　 分析：(1)显然方程的左边不是一个完全平方式，因此，要按前面的方法化为完全平方式；(2)同上．

　　 解：(1)x²-2x=35　 x²-2x+1²=35+1　 (x-1)²=36　 x-1=±6

　　　　 x-1=6，x-1=-6

　　　 　x₁=7，x₂=-5

　　 可以，验证x₁=7，x₂=-5都是x²+2x-35=0的两根．

　　 (2)x²-2x-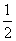=0　 x²-2x=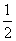

　　　　 x²-2x+1²=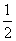+1　 (x-1)²=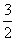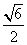

　　　　 x-1=±即x-1=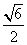，x-1=-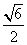

　　　 　x₁=1+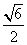，x₂=1-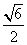

　　 可以验证：x₁=1+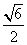，x₂=1-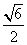都是方程的根．

　　 (学生活动)请同学们解下列方程

　　 (1)3x²-1=5　 (2)4(x-1)²-9=0　 (3)4x²+16x+16=9

　　 老师点评：上面的方程都能化成x²=p或(mx+n)²=p(p≥0)的形式，那么可得

x=±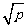或mx+n=±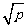(p≥0)．

　　 如：4x²+16x+16=(2x+4)²

3．在一次手工制作中，某同学准备了一根长4米的铁丝，由于需要，现在要制成一个矩形方框，并且要使面积尽可能大，你能帮助这名同学制成方框，并说明你制作的理由吗？

2．某农场要建一个长方形的养鸡场，鸡场的一边靠墙(墙长25m)，另三边用木栏围成，木栏长40m．

　　 (1)鸡场的面积能达到180m²吗？能达到200m吗？

　　 (2)鸡场的面积能达到210m²吗？

1．解关于x的方程(x+m)²=n．

3．如果a、b为实数，满足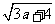+b²-12b+36=0，那么ab的值是_______．

2．如果方程2(x-3)²=72，那么，这个一元二次方程的两根是________．

1．若8x²-16=0，则x的值是_________．