
1.用公式法解方程4x2-12x=3,得到( ).
A.x=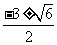 B.x=
B.x=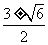
C.x=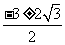 D.x=
D.x=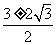
2.选用作业设计:
1.教材P45 复习巩固4.
本节课应掌握:
(1)求根公式的概念及其推导过程;
(2)公式法的概念;
(3)应用公式法解一元二次方程;
(4)初步了解一元二次方程根的情况.
例2.某数学兴趣小组对关于x的方程(m+1)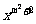 +(m-2)x-1=0提出了下列问题.
+(m-2)x-1=0提出了下列问题.
(1)若使方程为一元二次方程,m是否存在?若存在,求出m并解此方程.
(2)若使方程为一元二次方程m是否存在?若存在,请求出.
你能解决这个问题吗?
分析:能.(1)要使它为一元二次方程,必须满足m2+1=2,同时还要满足(m+1)≠0.
(2)要使它为一元一次方程,必须满足:
①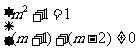 或②
或②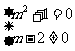 或③
或③
解:(1)存在.根据题意,得:m2+1=2
m2=1 m=±1
当m=1时,m+1=1+1=2≠0
当m=-1时,m+1=-1+1=0(不合题意,舍去)
∴当m=1时,方程为2x2-1-x=0
a=2,b=-1,c=-1
b2-4ac=(-1)2-4×2×(-1)=1+8=9
x=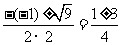
x1=,x2=-
因此,该方程是一元二次方程时,m=1,两根x1=1,x2=- .
.
(2)存在.根据题意,得:①m2+1=1,m2=0,m=0
因为当m=0时,(m+1)+(m-2)=2m-1=-1≠0
所以m=0满足题意.
②当m2+1=0,m不存在.
③当m+1=0,即m=-1时,m-2=-3≠0
所以m=-1也满足题意.
当m=0时,一元一次方程是x-2x-1=0,
解得:x=-1
当m=-1时,一元一次方程是-3x-1=0
解得x=-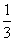
因此,当m=0或-1时,该方程是一元一次方程,并且当m=0时,其根为x=-1;当m=-1时,其一元一次方程的根为x=-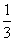 .
.
教材P42 练习1.(1)、(3)、(5)
如果这个一元二次方程是一般形式ax2+bx+c=0(a≠0),你能否用上面配方法的步骤求出它们的两根,请同学独立完成下面这个问题.
问题:已知ax2+bx+c=0(a≠0)且b2-4ac≥0,试推导它的两个根x1=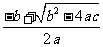 ,x2=
,x2=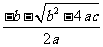
分析:因为前面具体数字已做得很多,我们现在不妨把a、b、c也当成一个具体数字,根据上面的解题步骤就可以一直推下去.
解:移项,得:ax2+bx=-c
二次项系数化为1,得x2+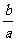 x=-
x=-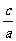
配方,得:x2+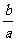 x+(
x+(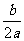 )2=-
)2=-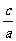 +(
+(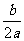 )2
)2
即(x+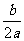 )2=
)2=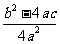
∵b2-4ac≥0且4a2>0
∴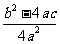 ≥0
≥0
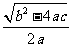
直接开平方,得:x+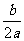 =±
=±
即x=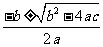
∴x1= ,x2=
,x2=
由上可知,一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定,因此:
(1)解一元二次方程时,可以先将方程化为一般形式ax2+bx+c=0,当b-4ac≥0时,将a、b、c代入式子x= 就得到方程的根.
就得到方程的根.
(2)这个式子叫做一元二次方程的求根公式.
(3)利用求根公式解一元二次方程的方法叫公式法.
(4)由求根公式可知,一元二次方程最多有两个实数根.
例1.用公式法解下列方程.
(1)2x2-4x-1=0 (2)5x+2=3x2
(3)(x-2)(3x-5)=0 (4)4x2-3x+1=0
分析:用公式法解一元二次方程,首先应把它化为一般形式,然后代入公式即可.
解:(1)a=2,b=-4,c=-1
b2-4ac=(-4)2-4×2×(-1)=24>0
x=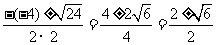
∴x1=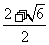 ,x2=
,x2=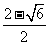
(2)将方程化为一般形式
3x2-5x-2=0
a=3,b=-5,c=-2
b2-4ac=(-5)2-4×3×(-2)=49>0
x=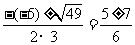
x1=2,x2=-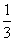
(3)将方程化为一般形式
3x2-11x+9=0
a=3,b=-11,c=9
b2-4ac=(-11)2-4×3×9=13>0
∴x=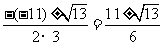
∴x1=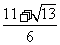 ,x2=
,x2=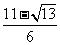
(3)a=4,b=-3,c=1
b2-4ac=(-3)2-4×4×1=-7<0
因为在实数范围内,负数不能开平方,所以方程无实数根.
(学生活动)用配方法解下列方程
(1)6x2-7x+1=0 (2)4x2-3x=52
(老师点评) (1)移项,得:6x2-7x=-1
二次项系数化为1,得:x2-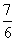 x=-
x=-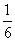
配方,得:x2-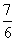 x+(
x+(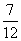 )2=-
)2=-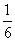 +(
+(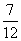 )2
)2
(x-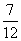 )2=
)2=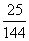
x-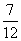 =±
=±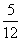 x1=
x1=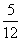 +
+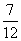 =
=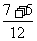 =1
=1
x2=-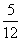 +
+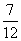 =
=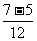 =
=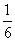
(2)略
总结用配方法解一元二次方程的步骤(学生总结,老师点评).
(1)移项;
(2)化二次项系数为1;
(3)方程两边都加上一次项系数的一半的平方;
(4)原方程变形为(x+m)2=n的形式;
(5)如果右边是非负数,就可以直接开平方求出方程的解,如果右边是负数,则一元二次方程无解.
3.新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达5000元,每台冰箱的定价应为多少元?
2.如果x2-4x+y2+6y+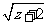 +13=0,求(xy)z的值.
+13=0,求(xy)z的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com