3．二次三项式x²+20x+96分解因式的结果为________；如果令x²+20x+96=0，那么它的两个根是_________．

2．方程(2x-1)²=2x-1的根是________．

1．x²-5x因式分解结果为_______；2x(x-3)-5(x-3)因式分解的结果是______．

3．如果不为零的n是关于x的方程x²-mx+n=0的根，那么m-n的值为(　 )．

　　　 A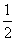．-　　 B．-1　　　 C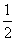．　　 D．1

2．下列命题①方程kx²-x-2=0是一元二次方程；②x=1与方程x²=1是同解方程；③方程x²=x与方程x=1是同解方程；④由(x+1)(x-1)=3可得x+1=3或x-1=3，其中正确的命题有(　 )．

　　　 A．0个　　 B．1个　　 C．2个　　 D．3个

1．下面一元二次方程解法中，正确的是(　 )．

　　　 A．(x-3)(x-5)=10×2，∴x-3=10，x-5=2，∴x₁=13，x₂=7

　　　 B．(2-5x)+(5x-2)²=0，∴(5x-2)(5x-3)=0，∴x₁= ，x₂=

　　　 C．(x+2)²+4x=0，∴x₁=2，x₂=-2

　　　 D．x²=x　 两边同除以x，得x=1

　　 教材P₄₆　 复习巩固5　 综合运用8、10　 拓广探索11．

　　　　　 第六课时作业设计

　　 本节课要掌握：

　　 (1)用因式分解法，即用提取公因式法、十字相乘法等解一元二次方程及其应用．

　　 (2)三种方法(配方法、公式法、因式分解法)的联系与区别：

　　 联系①降次，即它的解题的基本思想是：将二次方程化为一次方程，即降次．

　　 ②公式法是由配方法推导而得到．

　　 ③配方法、公式法适用于所有一元二次方程，因式分解法适用于某些一元二次方程．

　　 区别：①配方法要先配方，再开方求根．

　　 ②公式法直接利用公式求根．

　　 ③因式分解法要使方程一边为两个一次因式相乘，另一边为0，再分别使各一次因式等于0．

　　 例3．我们知道x²-(a+b)x+ab=(x-a)(x-b)，那么x²-(a+b)x+ab=0就可转化为(x-a)(x-b)=0，请你用上面的方法解下列方程．

　　 (1)x²-3x-4=0　　 (2)x²-7x+6=0　 (3)x²+4x-5=0

　　 分析：二次三项式x²-(a+b)x+ab的最大特点是x²项是由x·x而成，常数项ab是由-a·(-b)而成的，而一次项是由-a·x+(-b·x)交叉相乘而成的．根据上面的分析，我们可以对上面的三题分解因式．

　　 解(1)∵x²-3x-4=(x-4)(x+1)

　　 ∴(x-4)(x+1)=0

　　 ∴x-4=0或x+1=0

　　 ∴x₁=4，x₂=-1

　　 (2)∵x²-7x+6=(x-6)(x-1)

　　 ∴(x-6)(x-1)=0

　　 ∴x-6=0或x-1=0

　　 ∴x₁=6，x₂=1

　　 (3)∵x²+4x-5=(x+5)(x-1)

　　 ∴(x+5)(x-1)=0

　　 ∴x+5=0或x-1=0

　　 ∴x₁=-5，x₂=1

　　 上面这种方法，我们把它称为十字相乘法．

　　 教材P₄₅　 练习1、2．