
2.方程3x2+9=0的根为( ).
A.3 B.-3 C.±3 D.无实数根
1.若x2-4x+p=(x+q)2,那么p、q的值分别是( ).
A.p=4,q=2 B.p=4,q=-2 C.p=-4,q=2 D.p=-4,q=-2
2.选用作业设计:
1.教材P45 复习巩固1、2.
本节课应掌握:
由应用直接开平方法解形如x2=p(p≥0),那么x=±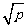 转化为应用直接开平方法解形如(mx+n)2=p(p≥0),那么mx+n=±
转化为应用直接开平方法解形如(mx+n)2=p(p≥0),那么mx+n=±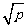 ,达到降次转化之目的.
,达到降次转化之目的.
例3.某公司一月份营业额为1万元,第一季度总营业额为3.31万元,求该公司二、三月份营业额平均增长率是多少?
分析:设该公司二、三月份营业额平均增长率为x,那么二月份的营业额就应该是(1+x),三月份的营业额是在二月份的基础上再增长的,应是(1+x)2.
解:设该公司二、三月份营业额平均增长率为x.
那么1+(1+x)+(1+x)2=3.31
把(1+x)当成一个数,配方得:
(1+x+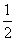 )2=2.56,即(x+
)2=2.56,即(x+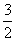 )2=2.56
)2=2.56
x+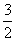 =±1.6,即x+
=±1.6,即x+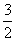 =1.6,x+
=1.6,x+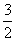 =-1.6
=-1.6
方程的根为x1=10%,x2=-3.1
因为增长率为正数,
所以该公司二、三月份营业额平均增长率为10%.
教材P36 练习.
上面我们已经讲了x2=8,根据平方根的意义,直接开平方得x=±2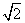 ,如果x换元为2t+1,即(2t+1)2=8,能否也用直接开平方的方法求解呢?
,如果x换元为2t+1,即(2t+1)2=8,能否也用直接开平方的方法求解呢?
(学生分组讨论)
老师点评:回答是肯定的,把2t+1变为上面的x,那么2t+1=±2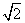
即2t+1=2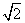 ,2t+1=-2
,2t+1=-2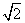
方程的两根为t1=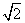 -
-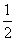 ,t2=-
,t2=-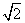 -
-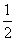
例1:解方程:x2+4x+4=1
分析:很清楚,x2+4x+4是一个完全平方公式,那么原方程就转化为(x+2)2=1.
解:由已知,得:(x+2)2=1
直接开平方,得:x+2=±1
即x+2=1,x+2=-1
所以,方程的两根x1=-1,x2=-3
例2.市政府计划2年内将人均住房面积由现在的10m2提高到14.4m,求每年人均住房面积增长率.
分析:设每年人均住房面积增长率为x.一年后人均住房面积就应该是10+10x=10(1+x);二年后人均住房面积就应该是10(1+x)+10(1+x)x=10(1+x)2
解:设每年人均住房面积增长率为x,
则:10(1+x)2=14.4
(1+x)2=1.44
直接开平方,得1+x=±1.2
即1+x=1.2,1+x=-1.2
所以,方程的两根是x1=0.2=20%,x2=-2.2
因为每年人均住房面积的增长率应为正的,因此,x2=-2.2应舍去.
所以,每年人均住房面积增长率应为20%.
(学生小结)老师引导提问:解一元二次方程,它们的共同特点是什么?
共同特点:把一个一元二次方程“降次”,转化为两个一元一次方程.我们把这种思想称为“降次转化思想”.
学生活动:请同学们完成下列各题
问题1.填空
(1)x2-8x+______=(x-______)2;(2)9x2+12x+_____=(3x+_____)2;(3)x2+px+_____=(x+______)2.
问题2.如图,在△ABC中,∠B=90°,点P从点B开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动,如果AB=6cm,BC=12cm,P、Q都从B点同时出发,几秒后△PBQ的面积等于8cm2?

老师点评:
问题1:根据完全平方公式可得:(1)16
4;(2)4 2;(3)(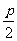 )2
)2 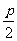 .
.
问题2:设x秒后△PBQ的面积等于8cm2
则PB=x,BQ=2x
依题意,得: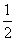 x·2x=8
x·2x=8
x2=8
根据平方根的意义,得x=±2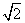
即x1=2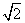 ,x2=-2
,x2=-2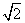
可以验证,2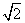 和-2
和-2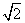 都是方程
都是方程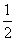 x·2x=8的两根,但是移动时间不能是负值.
x·2x=8的两根,但是移动时间不能是负值.
所以2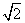 秒后△PBQ的面积等于8cm2.
秒后△PBQ的面积等于8cm2.
P37 练习1、2
小结:
关于量的变化率问题,不管是增加还是减少,都是变化前的数据为基础,每次按相同的百分数变化,若原始数据为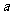 ,设平均变化率为
,设平均变化率为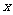 ,经第一次变化后数据为
,经第一次变化后数据为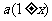 ;经第二次变化后数据为
;经第二次变化后数据为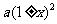 。在依题意列出方程并解得
。在依题意列出方程并解得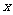 值后,还要依据
值后,还要依据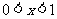 的条件,做符合题意的解答。
的条件,做符合题意的解答。
作业:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com