
4.三个连续奇数,两两相乘后再相加,其和为359,求这三个数.
3.某工厂计划经过两年的时间将某种产品的产量从每年144万台提高到169万台,则每年平均约增长( )
A.5% B.8% C.10% D.15%
2.某型号的手机连续两次降价,每个售价由原来的1 185元降到了580元.设平均每次降价的百分率为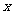 ,则列出方程正确的是( )
,则列出方程正确的是( )
A.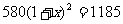 B.
B.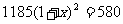
C.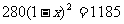 D.
D.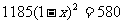
1.已知两个连续偶数的积是168,则较大的偶数为( )
A.12 B.14 C.16 D.18
一元二次方程的应用是中考数学重点考查的内容之一,它的试题背景与二元一次方程组的应用、简单分式方程的应用、一元一次方程的应用一样,随着改革的继续而更富有时代的气息,更宣于生活化,更贴近学生的实际.
[解题指导]
例1.将进货单价为40元的商品按50元售出时,就能卖出500个.已知这种商品每个涨价1元,其销售量就减少10个,问为了赚得8000元的利润,售价应定为多少?这时应进货多少个?
分析:如果按单价50元售出,每个利润是10元,卖出500个,只能赚得5000元.为了赚得8000只.只能涨价,但要适度,否则销售量就少得太多.其中的等量关系是:每个商品的利润×销售量=8000(元).这里的关键是如何表示出每个商品的利润和销售量的问题.
解:设商品的单价是 元,则每个商品的利润是
元,则每个商品的利润是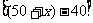 元,销售量是
元,销售量是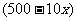 个.
个.
由题意列方程为
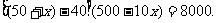
整理,得 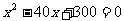 .
.
解方程,得 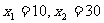 .
.
故商品的的单价可定为50+10=60元或50+30=80元.
当商品每个单价为60元时,其进货量只能是500-10×10=400个,当商品每个单价为80元时,其进货量只能是
500-10×30=200个.
答:售价定为60元时,进货是400个,售价定为80元时,进货是200个.
点评:此题属于能力要求较高的一元二次方程应用题.关键在于表示出两个“动态”的量:每个商品的利润、销售的量.
例2.某电脑公司2000年的各项经营收入中,经营电脑配件的收入为600万元,占全年经营总收入的40%,该公司预计2002年经营总收入要达到2160万元,且计划从2000年到2002年,每年经营总收入的年增长率相同,问2001年预计经营总收入为多少万元?
分析:运用基本关系式:基数(1+平均增长率)n=实际数.当然首先要求(或表示)出基数:=600÷40%.
解:设2001年预计经营总收入为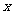 万元,每年经营总收入的年增长率为
万元,每年经营总收入的年增长率为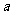 .
.
根据题意,得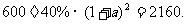
解方程,得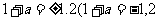 不合题意,舍去),
不合题意,舍去),
∴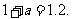
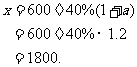
答:2001年预计经营总收入为1800万元.
点评:本题是有关增长率问题,它的基本关系式是:基数×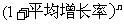 =实际数.
=实际数.
例3.某市供电公司规定,本公司职工,每户一个月用电量若不超过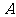 千瓦·时,则一个月的电费只要交10元,若超过
千瓦·时,则一个月的电费只要交10元,若超过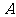 千瓦·时,则除了交10元外,超过部分每千瓦/时还要交
千瓦·时,则除了交10元外,超过部分每千瓦/时还要交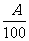 元.一户职工三月份用电80千瓦·时,交电费25元;四月份用电5千瓦·时,交电费10元,试求
元.一户职工三月份用电80千瓦·时,交电费25元;四月份用电5千瓦·时,交电费10元,试求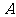 的值.
的值.
分析:本题需先判断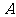 的范围,再建立等量关系:
的范围,再建立等量关系:
超过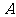 千瓦·时所交的钱+10元=25元.以此来作为解决问题的突破口.
千瓦·时所交的钱+10元=25元.以此来作为解决问题的突破口.
解:由题意,可知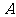 ≥45.
≥45.
且有
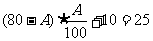 .
.
解得
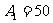 (千瓦·时),
(千瓦·时),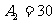 (不合题意,舍去).
(不合题意,舍去).
答: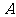 的值为50千瓦·时.
的值为50千瓦·时.
[自我测试]
1. 解一元二次方程的数学应用题的一般步骤
(1) 找--找出题中的等量关系
(2) 设--设未知数
(3) 列--列出方程,即根据找出的等量关系列出含有未知数的等式
(4) 解--解出所列的方程
(5) 验--将方程的解代入方程中检验,回到实际问题中检验
(6) 答--作答下结论
1.数学应用题
由实际情景加工整理成抽象实际的问题,通过数学化变成数学问题.经过求解、检验、修正改进等进而产生的问题称为数学应用问题,数学应用题是经过加工的数学应用问题,是呈现在我们中学生面前的数学应用问题.
从数学应用问题到数学应用题作了以下几个方面的“加工”.
(1) 加工“背景”:让背景材料为学生所熟悉的材料;让背景材料较为简洁.
(2) 加工“数学”:让“数学化”的过程较为简单,让各环节中使用的数学思想、方法和知识都是学生所能接受的.
(3) 加工“检验”:在问题中的检验和讨论“实际化”即检验数学结果是否合乎实际问题,有验证的意识就可以了.
6.(8分)小资料:财政预计,三峡工程投资需2039亿元,由静态投资901亿元、贷款利息成本a亿元、物价上涨价差(a+360)亿元三部分组成.但事实上,因国家调整利率,使贷款利息减少了15.4%;因物价上涨幅度比预测要低,使物价上涨价差减少了18.7%.
2004年三峡电站发电量为392亿度,预计2006年的发电量为564.48亿度,这两年的发电量年平均增长率相同.若发电量按此幅度增长,到2008年全部机组投入发电时,当年的发电量刚好达到三峡电站设计的最高年发电量.从2009年起,拟将三峡电站和葛洲坝电站的发电收益全部用于返还三峡工程投资成本.葛洲坝年发电量为270亿度,国家规定电站出售电价为0.25元/度.
(1)因利息调整和物价上涨幅度因素使三峡工程总投资减少多少亿元?(结果精确到1亿元)
(2)请你通过计算预测:大约到哪一年可以收回三峡工程的投资成本?
5.(6分) (2008义乌)义乌市是一个“车轮上的城市”,截止2007年底全市汽车拥有量为114508辆.己知
2005年底全市汽车拥有量为72983辆.请解答如下问题:
(1)2005年底至2007年底我市汽车拥有量的年平均增长率?(结果精确到0.1%)
(2)为保护城市环境,要求我市到2009年底汽车拥有量不超过158000辆,据估计从2007年底起,此后每年报废的汽车数量是上年底汽车拥有量的4%,那么每年新增汽车数量最多不超过多少辆?(假定每年新增汽车数量相同,结果精确到个位)
4.(8分)将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com