
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图3-9-4所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为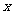 cm,那么
cm,那么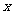 满足的方程是( )
满足的方程是( )
A.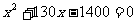 B.
B.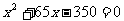
C.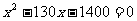 C.
C.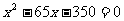
1.直角三角形的面积是30,两直角边的和是17,则斜边长为( )
 A.17
B.26
C.30
D.13
A.17
B.26
C.30
D.13
3.每件商品的成本是120元,试销了一阶段后,发现每件售价(元)与产品的日销售量(件)始终存在下表中的数量关系,但每天的盈利(元)却不一样.为找到每件产品的最佳定价,商场经理请一位营销策划员通过计算,在不改变每件售价(元)与日销售量(件)之间数量关系的情况下,每件定价为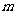 元时,每日盈利可达到最佳数1600元.若请你做这位营销策划员,
元时,每日盈利可达到最佳数1600元.若请你做这位营销策划员,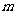 的值应是几?
的值应是几?
|
每件售价(元) |
130 |
150 |
165 |
|
每日销售(件) |
70 |
50 |
35 |
§3.9 一元二次方程的应用(二)
[解题指导]
 例1.如图3-9-1所示,某小区规划在一个长为40米,宽为26米的矩形场地
例1.如图3-9-1所示,某小区规划在一个长为40米,宽为26米的矩形场地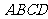 上修建三条同样宽的甬路,使其中两条与
上修建三条同样宽的甬路,使其中两条与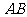 平行,另一条与
平行,另一条与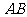 垂直,其余部分种草,若使每一块草坪的面积都为144米2,求甬路的宽度?
垂直,其余部分种草,若使每一块草坪的面积都为144米2,求甬路的宽度?
分析:为了使问题简化,不妨把种小块矩形草坪平移后拼成一大块矩形草整体思考,问题便显得轻而易举.
解:可设甬路宽为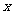 米,依题意,得
米,依题意,得
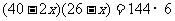 ,解得
,解得 (不合题意,舍去).
(不合题意,舍去).
答:甬路的宽度为2米.
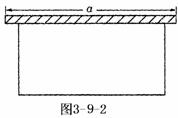 例2.如图3-9-2所示要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为
例2.如图3-9-2所示要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为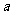 m,另三边用竹篱笆围成,已知篱笆总长为35m.
m,另三边用竹篱笆围成,已知篱笆总长为35m.
(1)求鸡场的长与宽各为多少米?
(2)题中的墙长度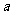 m对题目的解起着怎样的作用?
m对题目的解起着怎样的作用?
分析:从几何图形建立等量关系式.从所列得的方程的解、分类讨论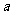 的不同取值所产生的影响.
的不同取值所产生的影响.
解:(1)设鸡场的宽为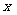 m,则长为
m,则长为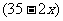 m.依题意列方程为
m.依题意列方程为
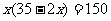 .
.
整理,得 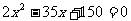 .
.
解方程,得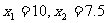 .
.
所以当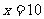 时,
时,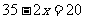 .
.
答:当鸡场的宽为10m时,长为15m;当鸡场宽为7.5m时,长为20m.
(2)由(1)解得结果可知:题中墙长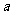 m对题目的解起严格的限制作用.当
m对题目的解起严格的限制作用.当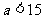 时,问题无解;当
时,问题无解;当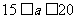 时,问题只有一解,即可建宽为10m,长为15m的一种鸡场;当
时,问题只有一解,即可建宽为10m,长为15m的一种鸡场;当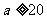 时,问题有两解.
时,问题有两解.
点评:应注意讨论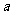 对题目的解起的关键作用.
对题目的解起的关键作用.
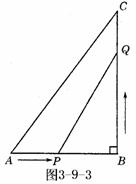 例3.已知:如图3-9-3所示,在△
例3.已知:如图3-9-3所示,在△ 中,
中,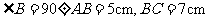 .点
.点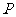 从点
从点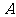 开始沿
开始沿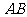 边向点
边向点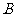 以1cm/s的速度移动,点
以1cm/s的速度移动,点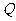 从点
从点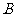 开始沿
开始沿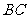 边向点
边向点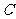 以2cm/s的速度移动.
以2cm/s的速度移动.
(1)如果 分别从
分别从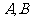 同时出发,那么几秒后,△
同时出发,那么几秒后,△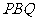 的面积等于4cm2?
的面积等于4cm2?
(2)如果 分别从
分别从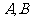 同时出发,那么几秒后,
同时出发,那么几秒后,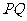 的长度等于5cm?
的长度等于5cm?
(3)在(1)中,△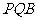 的面积能否等于7cm2?说明理由.
的面积能否等于7cm2?说明理由.
分析:设出未知数后,关键是用含未知数的代数式表示与问题有关的线段、面积等.
解 (1)设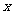 s后,△
s后,△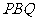 的面积等于4cm2,此时,
的面积等于4cm2,此时,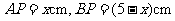 ,
,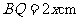 .
.
由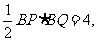 得
得
 .
.
整理,得 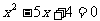 .
.
解方程,得 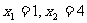 .
.
当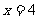 时,
时,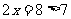 ,说明此时点
,说明此时点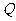 越过点
越过点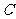 ,不合要求.
,不合要求.
答:1s后,△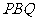 的面积等于4cm2.
的面积等于4cm2.
(2)仿(1),由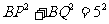 得
得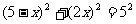 .
.
整理,得 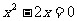
解方程,得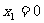 (不合,舍去),
(不合,舍去),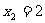 .
.
答:2s后,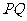 的长度等于5cm.
的长度等于5cm.
(3)仿(1),得
整理,得 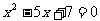
容易判断此方程无解.
答:△ 的面积不可能等于7cm2.
的面积不可能等于7cm2.
点评:较为复杂的一元二次方程在几何(图形)上的应用,往往要借用一些几何知识,如:面积公式;勾股定理;其它乘积关系的几何定理等等.观察图形,寻找等量关系,列出方程是解这类问题的关键.
[自我测试]
2. 某百货商店服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装每降价4元,那么平均每天就可多售出8件.要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
1.在一次庆典上,几个老同学互送纪念品一件,共送出72件纪念品,这些老同学共有几人?
9.某商店进了一批服装,进价为每件50元.按每件60元出售时,可销售800件;若单价每提高1元,则其销售量就减少20件.今商店计划获利12000元,问销售单价应定为多少元?此时应进多少件服装?
8.某人将2000元人民币按一年定期存入银行,到期后支取1000元购物,剩下1000元及应得利息又全部按一年定期存入银行,若存款利率不变,到期后得本金和利息共1320元,求这种存款方式的年利率.
7.某企业向银行贷款200万元开发新产品,一年后还贷款100万元,第二年后共还贷款及付息132万元.贷款均按一年期计算,年利率不变.求这种贷款的年利率.
6.王先生将三年前购置的一辆当时售价为28万元的汽车在汽车交易市场出售,得款17.5万元(含交易手续费及税金),已知第一年的折旧率为20%,求后两年的平均折旧率是多少?(精确到0.1%)
5.某工厂今年1月份产品数是50万件,要求3月份达到72万件,求这个工厂2月份和3月份的月平均增长率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com