
已知 =2-
=2-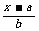 ,其中a、b是实数,且a+b≠0,
,其中a、b是实数,且a+b≠0,
化简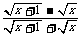 +
+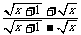 ,并求值.
,并求值.
分析:由于(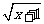 +
+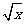 )(
)(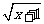 -
-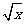 )=1,因此对代数式的化简,可先将分母有理化,再通过解含有字母系数的一元一次方程得到x的值,代入化简得结果即可.
)=1,因此对代数式的化简,可先将分母有理化,再通过解含有字母系数的一元一次方程得到x的值,代入化简得结果即可.
解:原式=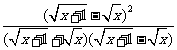 +
+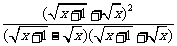
=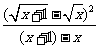 +
+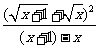
=(x+1)+x-2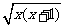 +x+2
+x+2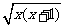
=4x+2
∵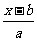 =2-
=2-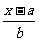 ∴b(x-b)=2ab-a(x-a) ∴bx-b2=2ab-ax+a2
∴b(x-b)=2ab-a(x-a) ∴bx-b2=2ab-ax+a2
∴(a+b)x=a2+2ab+b2 ∴(a+b)x=(a+b)2 ∵a+b≠0 ∴x=a+b
∴原式=4x+2=4(a+b)+2
2.计算
(1)(2x+3y)(2x-3y) (2)(2x+1)2+(2x-1)2
老师点评:这些内容是对八年级上册整式运算的再现.它主要有(1)单项式×单项式;(2)单项式×多项式;(3)多项式÷单项式;(4)完全平方公式;(5)平方差公式的运用.
如果把上面的x、y、z改写成二次根式呢?以上的运算规律是否仍成立呢?仍成立.
整式运算中的x、y、z是一种字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算规律也适用于二次根式.
自探2.计算:
(1)(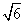 +
+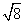 )×
)× (2)(4
(2)(4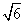 -3
-3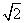 )÷2
)÷2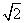
分析:刚才已经分析,二次根式仍然满足整式的运算规律,所以直接可用整式的运算规律.
自探3. 计算:
(1)(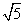 +6)(3-
+6)(3-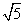 ) (2)(
) (2)(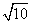 +
+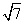 )(
)(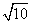 -
-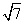 )
)
分析:刚才已经分析,二次根式的多项式乘以多项式运算在乘法公式运算中仍然成立.
自探1.(学生活动):请同学们完成下列各题:
1.计算
(1)(2x+y)·zx (2)(2x2y+3xy2)÷xy
2.同学们,我们以前学过完全平方公式a2±2ab+b2=(a±b)2,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的正数(包括0)都可以看作是一个数的平方,如3=(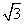 )2,5=(
)2,5=(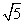 )2,你知道是谁的二次根式呢?下面我们观察: (
)2,你知道是谁的二次根式呢?下面我们观察: (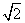 -1)2=(
-1)2=(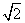 )2-2·1·
)2-2·1·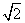 +12=2-2
+12=2-2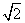 +1=3-2
+1=3-2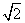 反之,3-2
反之,3-2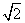 =2-2
=2-2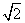 +1=(
+1=(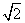 -1)2 ∴3-2
-1)2 ∴3-2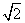 =(
=(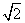 -1)2
-1)2
∴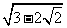 =
=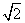 -1
-1
求:(1)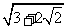 ; (2)
; (2)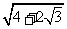 ;(3)你会算
;(3)你会算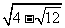 吗?
吗?
(4)若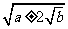 =
=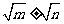 ,则m、n与a、b的关系是什么?并说明理由.
,则m、n与a、b的关系是什么?并说明理由.
教后反思:
1.若最简二次根式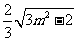 与
与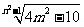 是同类二次根式,求m、n的值.
是同类二次根式,求m、n的值.
2.已知等腰直角三角形的直角边的边长为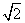 ,那么这个等腰直角三角形的周长是________.(结果用最简二次根式)
,那么这个等腰直角三角形的周长是________.(结果用最简二次根式)
1.某地有一长方形鱼塘,已知鱼塘的长是宽的2倍,它的面积是1600m2,鱼塘的宽是_______m.(结果用最简二次根式)
2.小明想自己钉一个长与宽分别为30cm和20cm的长方形的木框,为了增加其稳定性,他沿长方形的对角线又钉上了一根木条,木条的长应为( )米.(结果同最简二次根式表示)
A.13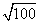 B.
B.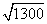 C.10
C.10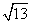 D.5
D.5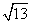
1.已知直角三角形的两条直角边的长分别为5和5,那么斜边的长应为( ).(结果用最简二次根式)
A.5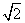 B.
B.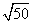 C.2
C.2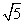 D.以上都不对
D.以上都不对
本节课应掌握运用最简二次根式的合并原理解决实际问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com