
3.某商场的标价比成本高p%,当该商品降价出售时,为了不亏损成本,售价的折扣(即降低的百分数)不得超过d%,则d可用p表示为( ).
A.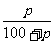 B.p C.
B.p C.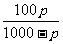 D.
D.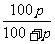
2.一台电视机成本价为a元,销售价比成本价增加25%,因库存积压,所以就按销售价的70%出售,那么每台售价为( ).
A.(1+25%)(1+70%)a元 B.70%(1+25%)a元
C.(1+25%)(1-70%)a元 D.(1+25%+70%)a元
1.2005年一月份越南发生禽流感的养鸡场100家,后来二、三月份新发生禽流感的养鸡场共250家,设二、三月份平均每月禽流感的感染率为x,依题意列出的方程是( ).
A.100(1+x)2=250 B.100(1+x)+100(1+x)2=250
C.100(1-x)2=250 D.100(1+x)2
2.选用作业设计.
作业设计
1.教材P53 复习巩固1 综合运用1.
本节课应掌握:
利用“倍数关系”建立关于一元二次方程的数学模型,并利用恰当方法解它.
例2.某人将2000元人民币按一年定期存入银行,到期后支取1000元用于购物,剩下的1000元及应得利息又全部按一年定期存入银行,若存款的利率不变,到期后本金和利息共1320元,求这种存款方式的年利率.
分析:设这种存款方式的年利率为x,第一次存2000元取1000元,剩下的本金和利息是1000+2000x·80%;第二次存,本金就变为1000+2000x·80%,其它依此类推.
解:设这种存款方式的年利率为x
则:1000+2000x·80%+(1000+2000x·8%)x·80%=1320
整理,得:1280x2+800x+1600x=320,即8x2+15x-2=0
解得:x1=-2(不符,舍去),x2=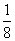 =0.125=12.5%
=0.125=12.5%
答:所求的年利率是12.5%.
(1)某林场现有木材a立方米,预计在今后两年内年平均增长p%,那么两年后该林场有木材多少立方米?
(2)某化工厂今年一月份生产化工原料15万吨,通过优化管理,产量逐年上升,第一季度共生产化工原料60万吨,设二、三月份平均增长的百分率相同,均为x,可列出方程为__________.
上面这道题大家都做得很好,这是一种利用二元一次方程组的数量关系建立的数学模型,那么还有没有利用其它形式,也就是利用我们前面所学过的一元二次方程建立数学模型解应用题呢?请同学们完成下面问题.
(学生活动)问题2:某工厂第一季度的一月份生产电视机是1万台,第一季度生产电视机的总台数是3.31万台,求二月份、三月份生产电视机平均增长的百分率是多少?
老师点评分析:直接假设二月份、三月份生产电视机平均增长率为x.因为一月份是1万台,那么二月份应是(1+x)台,三月份应是在二月份的基础上以二月份比一月份增长的同样“倍数”增长,即(1+x)+(1+x)x=(1+x)2,那么就很容易从第一季度总台数列出等式.
解:设二月份、三月份生产电视机平均增长的百分率为x,则1+(1+x)+(1+x)2=3.31
去括号:1+1+x+1+2x+x2=3.31
整理,得:x2+3x-0.31=0
解得:x=10%
答:(略)
以上这一道题与我们以前所学的一元一次、二元一次方程(组)、分式方程等为背景建立数学模型是一样的,而我们借助的是一元二次方程为背景建立数学模型来分析实际问题和解决问题的类型.
例1.某电脑公司2001年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
分析:设这个增长率为x,由一月份的营业额就可列出用x表示的二、三月份的营业额,又由三月份的总营业额列出等量关系.
解:设平均增长率为x
则200+200(1+x)+200(1+x)2=950
整理,得:x2+3x-1.75=0
解得:x=50%
答:所求的增长率为50%.
(学生活动)问题1:列方程解应用题
下表是某一周甲、乙两种股票每天每股的收盘价(收盘价:股票每天交易结果时的价格):
|
星期 |
一 |
二 |
三 |
四 |
五 |
|
甲 |
12元 |
12.5元 |
12.9元 |
12.45元 |
12.75元 |
|
乙 |
13.5元 |
13.3元 |
13.9元 |
13.4元 |
13.75元 |
某人在这周内持有若干甲、乙两种股票,若按照两种股票每天的收盘价计算(不计手续费、税费等),则在他帐户上,星期二比星期一增加200元,星期三比星期二增加1300元,这人持有的甲、乙股票各多少股?
老师点评分析:一般用直接设元,即问什么就设什么,即设这人持有的甲、乙股票各x、y张,由于从表中知道每天每股的收盘价,因此,两种股票当天的帐户总数就是x或y乘以相应的每天每股的收盘价,再根据已知的等量关系;星期二比星期一增加200元,星期三比星期二增加1300元,便可列出等式.
解:设这人持有的甲、乙股票各x、y张.
则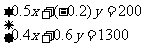 解得
解得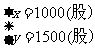
答:(略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com