
本节课应掌握:
建立多种一元二次方程的数学建模以解决如何全面地比较几个对象的变化状况的问题.
例3.某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的关系式.
(3)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
分析:(1)销售单价定为55元,比原来的销售价50元提高5元,因此,销售量就减少5×10kg.
(2)销售利润y=(销售单价x-销售成本40)×销售量[500-10(x-50)]
(3)月销售成本不超过10000元,那么销售量就不超过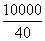 =250kg,在这个提前下,求月销售利润达到8000元,销售单价应为多少.
=250kg,在这个提前下,求月销售利润达到8000元,销售单价应为多少.
解:(1)销售量:500-5×10=450(kg);销售利润:450×(55-40)=450×15=6750元
(2)y=(x-40)[500-10(x-50)]=-10x2+1400x-40000
(3)由于水产品不超过10000÷40=250kg,定价为x元,则(x-400)[500-10(x-50)]=8000
解得:x1=80,x2=60
当x1=80时,进货500-10(80-50)=200kg<250kg,满足题意.
当x2=60时,进货500-10(60-50)=400kg>250kg,(舍去).
新华商场销售甲、乙两种冰箱,甲种冰箱每台进货价为2500元,市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.乙种冰箱每台进货价为2000元,市场调研表明:当销售价为2500元时,平均每天能售出8台;而当销售价每降低45元时,平均每天就能多售出4台,商场要想使这两种冰箱的销售利润平均每天达到5000元,那么两种冰箱的定价应各是多少?
刚才,我们分析了一种贺年卡原来平均每天可售出500张,每张盈利0.3元,为了减少库存降价销售,并知每降价0.1元,便可多售出100元,为了达到某个目的,每张贺年卡应降价多少元?如果本题中有两种贺年卡或者两种其它东西,量与量之间又有怎样的关系呢?即绝对量与相对量之间的关系.
例1.某商场礼品柜台春节期间购进甲、乙两种贺年卡,甲种贺年卡平均每天可售出500张,每张盈利0.3元,乙种贺年卡平均每天可售出200张,每张盈利0.75元,为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果甲种贺年卡的售价每降价0.1元,那么商场平均每天可多售出100张;如果乙种贺年卡的售价每降价0.25元,那么商场平均每天可多售出34张.如果商场要想每种贺年卡平均每天盈利120元,那么哪种贺年卡每张降价的绝对量大.
分析:原来,两种贺年卡平均每天的盈利一样多,都是150元;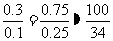 ,从这些数目看,好象两种贺年卡每张降价的绝对量一样大,下面我们就通过解题来说明这个问题.
,从这些数目看,好象两种贺年卡每张降价的绝对量一样大,下面我们就通过解题来说明这个问题.
解:(1)从“复习引入”中,我们可知,商场要想平均每天盈利120元,甲种贺年卡应降价0.1元.
(2)乙种贺年卡:设每张乙种贺年卡应降价y元,
则:(0.75-y)(200+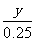 ×34)=120
×34)=120
即(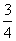 -y)(200+136y)=120
-y)(200+136y)=120
整理:得68y2+49y-15=0
y=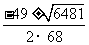
∴y≈-0.98(不符题意,应舍去)
y≈0.23元
答:乙种贺年卡每张降价的绝对量大.
因此,我们从以上一些绝对量的比较,不能说明其它绝对量或者相对量也有同样的变化规律.
(学生活动)例2.两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
老师点评:
绝对量:甲种药品成本的年平均下降额为(5000-3000)÷2=1000元,乙种药品成本的年平均下降额为(6000-3000)÷2=1200元,显然,乙种药品成本的年平均下降额较大.
相对量:从上面的绝对量的大小能否说明相对量的大小呢?也就是能否说明乙种药品成本的年平均下降率大呢?下面我们通过计算来说明这个问题.
解:设甲种药品成本的年平均下降率为x,
则一年后甲种药品成本为5000(1-x)元,两年后甲种药品成本为5000(1-x)元.
依题意,得5000(1-x)2=3000
解得:x1≈0.225,x2≈1.775(不合题意,舍去)
设乙种药品成本的平均下降率为y.
则:6000(1-y)2=3600
整理,得:(1-y)2=0.6
解得:y≈0.225
答:两种药品成本的年平均下降率一样大.
因此,虽然绝对量相差很多,但其相对量也可能相等.
(学生活动)请同学们独立完成下面的题目.
问题:某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元,为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?
老师点评:总利润=每件平均利润×总件数.设每张贺年卡应降价x元,则每件平均利润应是(0.3-x)元,总件数应是(500+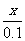 ×100)
×100)
解:设每张贺年卡应降价x元
则(0.3-x)(500+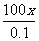 )=120
)=120
解得:x=0.1
答:每张贺年卡应降价0.1元.
3.某商场于第一年初投入50万元进行商品经营,以后每年年终将当年获得的利润与当年年初投入的资金相加所得的总资金,作为下一年年初投入的资金继续进行经营.
(1)如果第一年的年获利率为p,那么第一年年终的总资金是多少万元?(用代数式来表示)(注:年获利率= ×100%)
×100%)
(2)如果第二年的年获利率多10个百分点(即第二年的年获利率是第一年的年获利率与10%的和),第二年年终的总资金为66万元,求第一年的年获利率.
1.为了响应国家“退耕还林”,改变我省水土流失的严重现状,2000年我省某地退耕还林1600亩,计划到2002年一年退耕还林1936亩,问这两年平均每年退耕还林的平均增长率2.洛阳东方红拖拉机厂一月份生产甲、乙两种新型拖拉机,其中乙型16台,从二月份起,甲型每月增产10台,乙型每月按相同的增长率逐年递增,又知二月份甲、乙两型的产量之比是3:2,三月份甲、乙两型产量之和为65台,求乙型拖拉机每月的增长率及甲型拖拉机一月份的产量.
3.我国政府为了解决老百姓看病难的问题,决定下调药品价格,某种药品在1999年涨价30%后,2001年降价70%至a元,则这种药品在1999年涨价前价格是__________.
2.某糖厂2002年食糖产量为at,如果在以后两年平均增长的百分率为x,那么预计2004年的产量将是________.
1.某农户的粮食产量,平均每年的增长率为x,第一年的产量为6万kg,第二年的产量为_______kg,第三年的产量为_______,三年总产量为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com