
现在,我们根据刚才所复习的面积公式来建立一些数学模型,解决一些实际问题.
例1.某林场计划修一条长750m,断面为等腰梯形的渠道,断面面积为1.6m2,上口宽比渠深多2m,渠底比渠深多0.4m.
(1)渠道的上口宽与渠底宽各是多少?
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?
分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为x+2,渠底为x+0.4,那么,根据梯形的面积公式便可建模.
解:(1)设渠深为xm
则渠底为(x+0.4)m,上口宽为(x+2)m
依题意,得: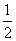 (x+2+x+0.4)x=1.6
(x+2+x+0.4)x=1.6
整理,得:5x2+6x-8=0
解得:x1=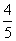 =0.8m,x2=-2(舍)
=0.8m,x2=-2(舍)
∴上口宽为2.8m,渠底为1.2m.
(2)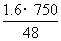 =25天
=25天
答:渠道的上口宽与渠底深各是2.8m和1.2m;需要25天才能挖完渠道.
学生活动:例2.如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?

老师点评:依据题意知:中央矩形的长宽之比等于封面的长宽之比=9:7,由此可以判定:上下边衬宽与左右边衬宽之比为9:7,设上、下边衬的宽均为9xcm,则左、右边衬的宽均为7xcm,依题意,得:中央矩形的长为(27-18x)cm,宽为(21-14x)cm.
因为四周的彩色边衬所点面积是封面面积的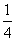 ,则中央矩形的面积是封面面积的.
,则中央矩形的面积是封面面积的.
所以(27-18x)(21-14x)= ×27×21
×27×21
整理,得:16x2-48x+9=0
解方程,得:x=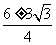 ,
,
x1≈2.8cm,x2≈0.2
所以:9x1=25.2cm(舍去),9x2=1.8cm,7x2=1.4cm
因此,上下边衬的宽均为1.8cm,左、右边衬的宽均为1.4cm.
6.圆的面积公式是什么?
(学生口答,老师点评)
5.平行四边形的面积公式是什么?
4.菱形的面积公式是什么?
3.梯形的面积公式是什么?
(口述)1.直角三角形的面积公式是什么?一般三角形的面积公式是什么呢?
2.正方形的面积公式是什么呢?长方形的面积公式又是什么?
3.某玩具厂有4个车间,某周是质量检查周,现每个车间都原有a(a>0)个成品,且每个车间每天都生产b(b>0)个成品,质量科派出若干名检验员周一、周二检验其中两个车间原有的和这两天生产的所有成品,然后,周三到周五检验另外两个车间原有的和本周生产的所有成品,假定每名检验员每天检验的成品数相同.
(1)这若干名检验员1天共检验多少个成品?(用含a、b的代数式表示)
(2)若一名检验员1天能检验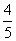 b个成品,则质量科至少要派出多少名检验员?
b个成品,则质量科至少要派出多少名检验员?
2.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加15.2%,那么应多种多少棵桃树?
1.上海甲商场七月份利润为100万元,九月份的利率为121万元,乙商场七月份利率为200万元,九月份的利润为288万元,那么哪个商场利润的年平均上升率较大?
3.一个容器盛满纯药液63L,第一次倒出一部分纯药液后用水加满,第二次又倒出同样多的药液,再加水补满,这时容器内剩下的纯药液是28L,设每次倒出液体xL,则列出的方程是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com