
1.教材P53 综合运用9 P58 复习题22 综合运用9.
本节课应掌握:
运用路程=速度×时间,建立一元二次方程的数学模型,并解决一些实际问题.
例3.如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)

分析:(1)因为依题意可知△ABC是等腰直角三角形,△DFC也是等腰直角三角形,AC可求,CD就可求,因此由勾股定理便可求DF的长.
(2)要求补给船航行的距离就是求DE的长度,DF已求,因此,只要在Rt△DEF中,由勾股定理即可求.
解:(1)连结DF,则DF⊥BC
∵AB⊥BC,AB=BC=200海里.
∴AC=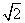 AB=200
AB=200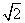 海里,∠C=45°
海里,∠C=45°
∴CD=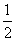 AC=100
AC=100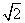 海里
海里
DF=CF,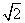 DF=CD
DF=CD
∴DF=CF=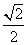 CD=
CD=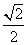 ×100
×100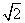 =100(海里)
=100(海里)
所以,小岛D和小岛F相距100海里.
(2)设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,
EF=AB+BC-(AB+BE)-CF=(300-2x)海里
在Rt△DEF中,根据勾股定理可得方程
x2=1002+(300-2x)2
整理,得3x2-1200x+100000=0
解这个方程,得:x1=200-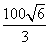 ≈118.4
≈118.4
x2=200+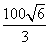 (不合题意,舍去)
(不合题意,舍去)
所以,相遇时补给船大约航行了118.4海里.
(1)同上题,求刹车后汽车行驶10m时约用了多少时间.(精确到0.1s)
(2)刹车后汽车行驶到20m时约用了多少时间.(精确到0.1s)
我们这一节课就是要利用同学们刚才所回答的“路程=速度×时间”来建立一元二次方程的数学模型,并且解决一些实际问题.
请思考下面的二道例题.
例1.某辆汽车在公路上行驶,它行驶的路程s(m)和时间t(s)之间的关系为:s=10t+3t2,那么行驶200m需要多长时间?
分析:这是一个加速运运,根据已知的路程求时间,因此,只要把s=200代入求关系t的一元二次方程即可.
解:当s=200时,3t2+10t=200,3t2+10t-200=0
解得t=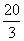 (s)
(s)
答:行驶200m需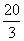 s.
s.
例2.一辆汽车以20m/s的速度行驶,司机发现前方路面有情况,紧急刹车后汽车又滑行25m后停车.
(1)从刹车到停车用了多少时间?
(2)从刹车到停车平均每秒车速减少多少?
(3)刹车后汽车滑行到15m时约用了多少时间(精确到0.1s)?
分析:(1)刚刹车时时速还是20m/s,以后逐渐减少,停车时时速为0.因为刹车以后,其速度的减少都是受摩擦力而造成的,所以可以理解是匀速的,因此,其平均速度为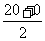 =10m/s,那么根据:路程=速度×时间,便可求出所求的时间.
=10m/s,那么根据:路程=速度×时间,便可求出所求的时间.
(2)很明显,刚要刹车时车速为20m/s,停车车速为0,车速减少值为20-0=20,因为车速减少值20,是在从刹车到停车所用的时间内完成的,所以20除以从刹车到停车的时间即可.
(3)设刹车后汽车滑行到15m时约用除以xs.由于平均每秒减少车速已从上题求出,所以便可求出滑行到15米的车速,从而可求出刹车到滑行到15m的平均速度,再根据:路程=速度×时间,便可求出x的值.
解:(1)从刹车到停车所用的路程是25m;从刹车到停车的平均车速是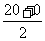 =10(m/s)
=10(m/s)
那么从刹车到停车所用的时间是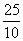 =2.5(s)
=2.5(s)
(2)从刹车到停车车速的减少值是20-0=20
从刹车到停车每秒平均车速减少值是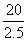 =8(m/s)
=8(m/s)
(3)设刹车后汽车滑行到15m时约用了xs,这时车速为(20-8x)m/s
则这段路程内的平均车速为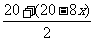 =(20-4x)m/s
=(20-4x)m/s
所以x(20-4x)=15
整理得:4x2-20x+15=0
解方程:得x=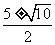
x1≈4.08(不合,舍去),x2≈0.9(s)
答:刹车后汽车行驶到15m时约用0.9s.
(老师口问,学生口答)路程、速度和时间三者的关系是什么?
3.谁能量出道路的宽度:
如图22-10,有矩形地ABCD一块,要在中央修一矩形花辅EFGH,使其面积为这块地面积的一半,且花圃四周道路的宽相等,今无测量工具,只有无刻度的足够长的绳子一条,如何量出道路的宽度?
请同学们利用自己掌握的数学知识来解决这个实际问题,相信你一定能行.

2.在一块长12m,宽8m的长方形平地中央,划出地方砌一个面积为8m2的长方形花台,要使花坛四周的宽地宽度一样,则这个宽度为多少?
1.如图所示的一防水坝的横截面(梯形),坝顶宽3m,背水坡度为1:2,迎水坡度为1:1,若坝长30m,完成大坝所用去的土方为4500m2,问水坝的高应是多少?(说明:背水坡度 =
=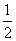 ,迎水坡度
,迎水坡度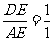 )(精确到0.1m)
)(精确到0.1m)

3.如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com