23.1 图形的旋转

活动目标:

⒈经历对生活中旋转现象的观察分析过程，引导学生用数学的眼光看待生活中的有关问题。

⒉通过具体实例认识旋转，知道旋转的性质。

⒊经历对具有旋转现象的图形的观察，操作，画图等过程，掌握好作图的基本技能。

活动重点：

　　 通过具体实例认识，知道旋转的性质。

活动难点：

　　 探索旋转的性质，并能应用性质掌握作图技能。

活动过程：

㈠ 情境创设

展示一些图片创设情境，让学生说说这些旋转现象有什么共同特征，还能不能再举出一些类似的例子？--从学生熟悉的生活现象入手，帮助学生通过具体实例认识旋转，理解旋转的基本涵义，同时引导学生用数学的观点看待生活中的有关问题，发展学生的数学观。

㈡ 探索活动

活动一：将△ ABC绕着点C旋转，记旋转后的三角形为△DEC。

　 问题1：你能说说BC旋转到了什么位置？AC旋转到了什么位置？

　 问题2：点A与哪个点对应？点B与哪个点对应呢？

　 问题3：旋转前与旋转后的两个三角形，什么发生了改变？又有哪些没有改变？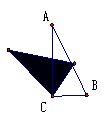　　　　　　　　　　　　　　　　

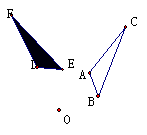
活动二：将△ABC绕着点O旋转，记旋转后有的三角形为△DEF。

问题1：你知道点A旋转到了哪个点的位置吗？点B呢？点C呢？

　 问题2：旋转前与旋转后的两个三角形，什么发生了改变？又有哪些没有改变？

问题：根据这两个活动，你知道什么叫做旋转吗？

活动一：观察旋转过程。

问题4：观察边AC的旋转痕迹，你能求出边AC旋转了多少度吗？BC呢？

　　　 A点旋转到D点，转了多少度？B 点转到E点，又转了多少度？

　问题5：如果继续旋转，你发现了什么？

活动二：演示旋转，仔细观察。

问题3：观察点C的旋转痕迹，你能测量出C点旋转了多少度吗？点A旋转了多少度？点B呢？

问题4：如果取AC的中点M，那么点M会旋转到什么位置？你能画出来吗？那点M旋转了多少度？再继续旋转，你发现了什么？

问题5：观察点C的旋转痕迹，你能说说点C是如何运动的吗？根据这个运动特点，

　　　　　 你能说说点C与对应点F有什么关系吗？点A与点D；点B与点E是否也具有这种关系？

讨论：你能说说旋转前与旋转后的两个之间有哪些会改变？又有哪些无论你怎么旋转，也不会改变？

㈢ 新授

定义：在平面内，将一个图形绕着一个定点旋转一定的角度，这样的图形运动就叫做图形的旋转。这个定点就叫旋转中心，旋转的角度就叫旋转角。图形的旋转不改变图形大小与形状。　　　　

性质：旋转前，旋转后的两个图形全等。

对应点到旋转中心的距离相等

每一对对应点与旋转中心的连线所成的角彼此相等　　　　　　　　　　　　　　　　　　　　

思考:已知图形的旋转,如何测量出旋转角呢?　　　　　　　　　　　　　　　　　　　　　　　　　　

㈣ 巩固练习　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

⒈如图,正方形A′B′C′D′是正方形ABCD按顺时针方向旋转一　　　　　　　　　　　　　　　　　　

定的角度而成的。请指出图中的哪一点是旋转中心?并度量旋转的角度。

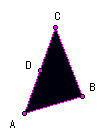
⒉⑴画出△ABC绕点A按逆时针方向旋转90°后的对应三角形。　　　　　　　　　　　　　　　　　　

⑵如果点D是AC的中点，那么经过上述旋转后，点D旋转到什么位置？　　　　　　　　　　　　　

请在所画图中将点D的对应点D′表示出来。

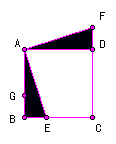
⒊如图，在正方形ABCD中，E是BC上一点，△ABE经旋转后得到△ADF。　　　　　　　　　　　

⑴旋转中心是哪一点？旋转了多少度？说说你是怎么测量的？　　　　　　　　　　　　　　　　　　

⑵如果G点是AB上的一点，点G应旋转到什么时候位置？　　　　　　　　　　　　　　　　　　　

请在图中将点G的对应点G′表示出来。

㈤ 操作训练　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　

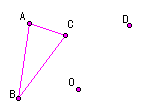
　 已知A点与点O，画出点A绕着点O旋转30°后的点A′　　　　　　　　　　　　　　　　　　　

　 拓展一：已知线段AB与点O，画出线段AB绕着点O按逆时针方向旋转80°后的图形。　　　　　　

　 拓展二：已知△ ABC和点O，画出△ ABC绕着点O按逆时针方向旋转80°后的图形。　　　　　　

　 拓展三：若改成多边形呢？你能总结出旋转作图的方法吗？

⒋思考:如图,△ABC绕着点O旋转后,点A到达点A′的位置,你画出旋转后的三角形吗?

㈥ 课堂小结：

通过本节课的学习,你知道什么是旋转了吗?你认为旋转有哪些性质?,你能作出符合

某一条件旋转后的图形吗?

2.用试验的方法探索情景一中所列方程x(x+10)=900的解，方程有几个解？都是情景一的解吗？突破难点

组1： 900=2×2×3×3×5×5

　　　 900=36×25 或 900=(-36)×(-25) ……

组2：

宽　　 　 …　 20 …　 30　 …　　 宽　　 …　 25 …　 26 …

长　　 …　 30 …　 40　 …　　 长　　 …　 35 …　 36 …

面积　　　 … 600 …　 1200 …　　 面积　　　 …　 875 … 936 …

宽　　 …　 25.4　 …　 25.5 …　 宽　　 　 … 25.41　　 …　　 25.42 …

长　　 …　 35.4　 …　 35.5 …　 长　　 　 … 35.41　　 …　　 35.42 …

面积　　　 …　 899.16 …　 905.25 …　 面积　　　 … 899.7681　 …　　 900.3746…

⑷归纳小结反思提高

小结：通过本节课的学习，你学到了哪些知识？请谈一谈体会和收获.

⑸布置作业分层落实

作 业：

基本题：教材 习题1、2、3；

拓展题：用试验的方法探索情景二中竹竿的长度！

附板书设计：

一元二次方程

一元二次方程的概念

　　　 一元二次方程的一般形式：

㈤说评价

课堂教学是一个动态过程，学生的思维又常常受到课堂气氛或突发事件的影响，为了达到最佳的教学效果，我将"教学反应"型评价和"教学反馈"型评价相结合，一方面根据课堂实施状况和学生反馈的信息而作出一种即时性评价，并顺势从教学内部进行调节；另一方面根据课堂练习的反馈，了解学生掌握知识的程度，灵活安排教学细节，从而达到教学的预期效果.

我说的就这些，不足之处请各位专家、老师批评指正！

1.将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项：

(及时巩固新知，为公式法的学习打下基础！)

2.能力目标：经历抽象一元二次方程的过程, 使学生体会出方程是刻画现实世界中数量关系的一个有效数学模型; 经历探索满足方程解的过程，发展估算的意识和能力.

1.知识目标：使学生充分了解一元二次方程的概念；正确掌握一元二次方程的一般形式.

7．根据题意，列出方程估算其解

在宽为20米，长为32米的矩形地面上，修筑同样宽的两条互相垂直的道路，余下的部分作为耕地的面积，要使此面积为540平方米，道路的宽应该是多少？

6．根据题意，列出方程(不必求解)

学校的一块长方形空地，长30米，宽22米，准备在中间开避花圃，四周修建等宽的林荫小道，使小道面积和花圃面积相等，求小道的宽。

5．当k取何值时，方程(k-1)x^k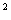+1+2kx+3=0是关于x的一元二次方程？

4．关于x的方程(m²-4)x²+(m-2)x+3m-1=0，当m______时，为一元一次方程，当m______时，为一元二次方程。