3．请独立完成下面的题目．

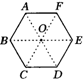
如图，O是六个正三角形的公共顶点，正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形？

　　 (老师点评)分析：能．看做是一条边(如线段AB)绕O点，按照同一方法连续旋转60°、120°、180°、240°、300°形成的．

　　 (学生活动)老师口问，学生口答．

1．什么叫旋转？什么叫旋转中心？什么叫旋转角？

　　 2．什么叫旋转的对应点？

　　 教材P65　 练习1、2、3．

3．第1、2两题有什么共同特点呢？

　　 共同特点是如果我们把时针、风车风轮当成一个图形，那么这些图形都可以绕着某一固定点转动一定的角度．

　　 像这样，把一个图形绕着某一点O转动一个角度的图形变换叫做旋转，点O叫做旋转中心，转动的角叫做旋转角．

　　 如果图形上的点P经过旋转变为点P′，那么这两个点叫做这个旋转的对应点．

　　 下面我们来运用这些概念来解决一些问题．

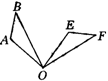
　 　例1．如图，如果把钟表的指针看做三角形OAB，它绕O点按顺时针方向旋转得到△OEF，在这个旋转过程中：

　　 (1)旋转中心是什么？旋转角是什么？

(2)经过旋转，点A、B分别移动到什么位置？

　　 解：(1)旋转中心是O，∠AOE、∠BOF等都是旋转角．

　　 (2)经过旋转，点A和点B分别移动到点E和点F的位置．

　　 例2．(学生活动)如图，四边形ABCD、四边形EFGH都是边长为1的正方形．

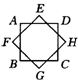　　 (1)这个图案可以看做是哪个“基本图案”通过旋转得到的？

　　 (2)请画出旋转中心和旋转角．

(3)指出，经过旋转，点A、B、C、D分别移到什么位置？

(老师点评)

(1)可以看做是由正方形ABCD的基本图案通过旋转而得到的．(2)画图略．(3)点A、点B、点C、点D移到的位置是点E、点F、点G、点H．

　　 最后强调，这个旋转中心是固定的，即正方形对角线的交点，但旋转角和对应点都是不唯一的．

2．再看我自制的好像风车风轮的玩具，它可以不停地转动．如何转到新的位置？(老师点评略)

3．圆是轴对称图形吗？等腰三角形呢？你还能指出其它的吗？

　　 (口述)老师点评并总结：

　　 (1)平移的有关概念及性质．

　　 (2)如何画一个图形关于一条直线(对称轴)的对称图形并口述它既有的一些性质．

　　 (3)什么叫轴对称图形？

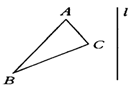
2．如图，已知△ABC和直线L，请你画出△ABC关于L的对称图形△A′B′C′．

　　 (学生活动)请同学们完成下面各题．

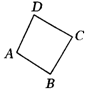
1．将如图所示的四边形ABCD平移，使点B的对应点为点D，作出平移后的图形．

23.1图形的旋转

教 学 过 程 设 计
问题与情境	师生行为	设计意图
(2)说出其中的对应点，对应角和对应线段. (3)旋转后图形的形状和大小是否发生变化.	本次活动中，教师应重点关注： (1)旋转的基本性质的探究过程应循序渐进，即演示→观察→猜想→讨论→归纳. (2)要给学生充足的时间和空间.
活动三 举例应用 加深认识 1、如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把ΔADE顺时针旋转90°，画出 旋转后的图形. 　 　A　　　　　 D 　 　　　　　　 E B　　　　　 C	学生动手练习，教师及时展示学生练习结果，并及时给予点评.	通过例题讲解，让学生加深对新知识的理解，培养学生分析问题和解决问题的能力.