
2.作出几个复合图形组成的图案旋转后的图案,要先求出图中的关键点──线的端点、角的顶点、圆的圆心等.
本节课应掌握:
1.选择不同的旋转中心、不同的旋转角,设计出美丽的图案;
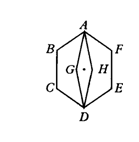 例3.如图,如何作出该图案绕O点按逆时针旋转90°的图形.
例3.如图,如何作出该图案绕O点按逆时针旋转90°的图形.
分析:该备案是一个比较复杂的图案,是作出几个复合图形组成的图案,因此,要先画出图中的关键点,这些关键点往往是图案里线的端点、角的顶点、圆的圆心等,然后再根据旋转的特征,作出这些关键点的对应点,最后再按原图案作出旋转后的图案.
解:(1)连结OA,过O点沿OA逆时针作∠AOA′=90°,在射线OA′上截取OA′=OA;
(2)用同样的方法分别求出B、C、D、E、F、G、H的对应点B′、C′、D′、E′、F′、G′、H′;
(3)作出对应线段A′B′、B′C′、C′D′、D′E′、E′F′、F′A′、A′G′、G′D′、D′H′、H′A′;
(4)所作出的图案就是所求的图案.
教材P65 练习.
2.旋转角不变,改变旋转中心
画出以下图,四边形ABCD分别为O、O为中心,旋转角都为30°的旋转图形.
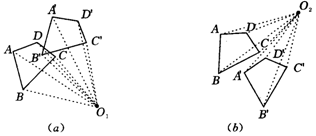
因此,从以上的画图中,我们可以得到旋转中心不变,改变旋转角与旋转角不变,改变旋转中心会产生不同的效果,所以,我们可以经过旋转设计出美丽的图案.
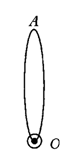 例1.如下图是菊花一叶和中心与圆圈,现以O为旋转中心画出分别旋转45°、90°、135°、180°、225°、270°、315°的菊花图案.
例1.如下图是菊花一叶和中心与圆圈,现以O为旋转中心画出分别旋转45°、90°、135°、180°、225°、270°、315°的菊花图案.
分析:只要以O为旋转中心、旋转角以上面为变化,旋转长度为菊花的最长OA,按菊花叶的形状画出即可.
解:(1)连结OA
(2)以O点为圆心,OA长为半径旋转45°,得A.
(3)依此类推画出旋转角分别为90°、135°、180°、225°、270°、315°的A、A、A、A、A、A.
(4)按菊花一叶图案画出各菊花一叶.
那么所画的图案就是绕O点旋转后的图形.
 例2.(学生活动)如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
例2.(学生活动)如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
老师点评:显然,画出后的图案不是菊花,而是另外的一种花了.
从上面的作图题中,我们知道,作图应满足三要素:旋转中心、旋转角、对应点,而旋转中心、旋转角固定下来,对应点就自然而然地固定下来.因此,下面就选择不同的旋转中心、不同的旋转角来进行研究.
1.旋转中心不变,改变旋转角
画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°的旋转图形.

2.请同学独立完成下面的作图题.
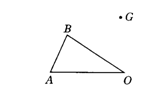 如图,△AOB绕O点旋转后,G点是B点的对应点,作出△AOB旋转后的三角形.
如图,△AOB绕O点旋转后,G点是B点的对应点,作出△AOB旋转后的三角形.
(老师点评)分析:要作出△AOB旋转后的三角形,应找出三方面:第一,旋转中心:O;第二,旋转角:∠BOG;第三,A点旋转后的对应点:A′.
1.(学生活动)老师口问,学生口答.
(1)各对应点到旋转中心的距离有何关系呢?
(2)各对应点与旋转中心所连线段的夹角与旋转角有何关系?
(3)两个图形是旋转前后的图形,它们全等吗?
3.旋转前、后的图形全等及其它们的应用.
2.对应点与旋转中心所连线段的夹角等于旋转角;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com