
(学生活动)请同学们完成下面三题.
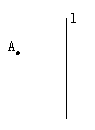
1.已知点A和直线L,如图,请画出点A关于L对称的点A′.
1.教材P74 综合运用5 P75 拓广探索8、9
2.应用中心对称图形解决有关问题.
本节课应掌握:
1.中心对称图形的有关概念;
例4.如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
分析:将矩形折叠,使C点和A点重合,折痕为EF,就是A、C两点关于O点对称,这方面的知识在解决一些翻折问题中起关键作用,对称点连线被对称轴垂直平分,进而转化为中垂线性质和勾股定理的应用,求线段长度或面积.
解:连接AF,
∵点C与点A重合,折痕为EF,即EF垂直平分AC.
∴AF=CF,AO=CO,∠FOC=90°,又四边形ABCD为矩形,∠B=90°,AB=CD=3,AD=BC=4
设CF=x,则AF=x,BF=4-x,
 由勾股定理,得AC2=BC2+AB2=52
由勾股定理,得AC2=BC2+AB2=52
∴AC=5,OC=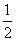 AC=
AC=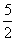
∵AB2+BF2=AF2 ∴32+(4-x)=2=x2
∴x=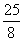
∵∠FOC=90°
∴OF2=FC2-OC2=(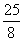 )2-(
)2-(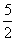 )2=(
)2=(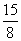 )2
OF=
)2
OF=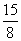
同理OE=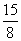 ,即EF=OE+OF=
,即EF=OE+OF=
教材P72 练习.
从另一个角度看,上面的(1)题就是将线段AB绕它的中点旋转180°,因为OA=OB,所以,就是线段AB绕它的中点旋转180°后与它重合.
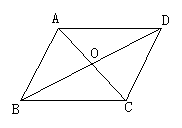 上面的(2)题,连结AD、BC,则刚才的两个关于中心对称的两个图形,就成平行四边形,如图所示.
上面的(2)题,连结AD、BC,则刚才的两个关于中心对称的两个图形,就成平行四边形,如图所示.
∵AO=OC,BO=OD,∠AOB=∠COD
∴△AOB≌△COD
∴AB=CD
也就是,ABCD绕它的两条对角线交点O旋转180°后与它本身重合.
因此,像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
(学生活动)例1:从刚才讲的线段、平行四边形都是中心对称图形外,每一位同学举出三个图形,它们也是中心对称图形.
老师点评:老师边提问学生边解答.
(学生活动)例2:请说出中心对称图形具有什么特点?
老师点评:中心对称图形具有匀称美观、平稳.
例3.求证:如图任何具有对称中心的四边形是平行四边形.

分析:中心对称图形的对称中心是对应点连线的交点,也是对应点间的线段中点,因此,直接可得到对角线互相平分.
证明:如图,O是四边形ABCD的对称中心,根据中心对称性质,线段AC、BD必过点O,且AO=CO,BO=DO,即四边形ABCD的对角线互相平分,因此,四边形ABCD是平行四边形.
2.(学生活动)作图题.
(1)作出线段AO关于O点的对称图形,如图所示.

(2)作出三角形AOB关于O点的对称图形,如图所示.
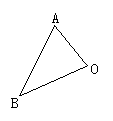
(2)延长AO使OC=AO,
延长BO使OD=BO,
连结CD
则△COD为所求的,如图所示.

1.(老师口问)口答:关于中心对称的两个图形具有什么性质?
(老师口述):关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
关于中心对称的两个图形是全等图形.
2.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
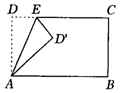 3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com