
2.关于中心对称的两个图形是全等图形.
例3.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.

 例4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和 四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
例4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和 四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
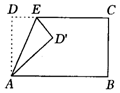 5.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
5.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
3.请同学任意画一三角形,以三角形一顶点为对称中心,画出这个三角形关于这个对称中心的对称图形,并分组讨论能得到什么结论.
(1)作△ABC一顶点为对称中心的对称图形;
(2)作关于一定点O为对称中心的对称图形.
因此,我们就得到 中心对称的性质:
2.各对称点绕O旋转180°后,这三点是否在一条直线上?
定义: 像这样,把一个图形___________________________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.
这两个图形中的对应点叫做关于中心的对称点.
例1.如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.

解:作法:(1)
(2)
(3)
答:(1)
(2)
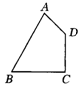
例2.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形.
问题:作出如图的两个图形绕点O旋转180°的图案,并回答下列的问题:
1.以O为旋转中心,旋转180°后两个图形是否重合?
 如图,△ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法.
如图,△ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法.
作法:(1)
(2)
(3)
(4)
即:△DEF就是所求作的三角形,如图所示.
教材P73 练习.
(学生活动)如图23-74,在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:
这些坐标与已知点的坐标有什么关系?
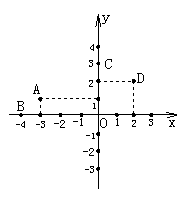
老师点评:画法:(1)连结AO并延长AO
(2)在射线AO上截取OA′=OA
(3)过A作AD′⊥x轴于D′点,过A′作A′D″⊥x轴于点D″.
∵△AD′O与△A′D″O全等
∴AD′=A′D″,OA=OA′
∴A′(3,-1)
同理可得B、C、D、E、F这些点关于原点的中心对称点的坐标.
(学生活动)分组讨论(每四人一组):讨论的内容:关于原点作中心对称时,①它们的横坐标与横坐标绝对值什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?
提问几个同学口述上面的问题.
老师点评:(1)从上可知,横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.(2)坐标符号相反,即设P(x,y)关于原点O的对称点P′(-x,-y).

例1.如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
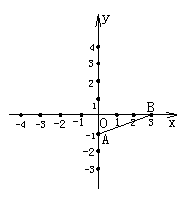
分析:要作出线段AB关于原点的对称线段,只要作出点A、点B关于原点的对称点A′、B′即可.
解:点P(x,y)关于原点的对称点为P′(-x,-y),
因此,线段AB的两个端点A(0,-1),B(3,0)关于原点的对称点分别为A′(1,0),B(-3,0).
连结A′B′.
则就可得到与线段AB关于原点对称的线段A′B′.
(学生活动)例2.已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
老师点评分析:先在直角坐标系中画出A、B、C三点并连结组成△ABC,要作出△ABC关于原点O的对称三角形,只需作出△ABC中的A、B、C三点关于原点的对称点,依次连结,便可得到所求作的△A′B′C′.
3.如图△ABO,绕点O旋转180°,画出旋转后的图形.

老师点评:老师通过巡查,根据学生解答情况进行点评.(略)
2. 如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com