2．教学难点：中心对称与中心对称图形的区别与联系．

1．教学重点：中心对称的概念和性质及中心对称图形的概念．

　观察、感受、讲解、类比

3.通过本节的学习，引导学生体验几何美，提高学习兴趣.

2.通过本节的学习，进一步培养学生的尺规作图能力.

1.了解中心对称、中心对称图形的概念，了解中心对称的性质.能找出线段、平行四边形的对称中心.会画出与已知图形成中心对称的图形.

这些坐标与已知点的坐标有什么关系？

　　 讨论：关于原点作中心对称时，①它们的横坐标与横坐标绝对值什么关系？纵坐标与纵坐标的绝对值又有什么关系？②坐标与坐标之间符号又有什么特点？

　 总结归纳：(1)从上可知，横坐标与横坐标的绝对值相等，纵坐标与纵坐标的绝对值相等．(2)坐标符号相反，即设P(x，y)关于原点O的对称点P′(-x，-y)．

　　 例1．如图，利用关于原点对称的点的坐标的特点，作出与线段AB关于原点对称的图形．

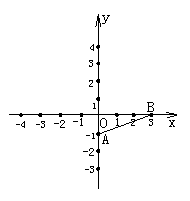
　　 解：点P(x，y)关于原点的对称点为P′(-x，-y)，

　　 因此，线段AB的两个端点A(0，-1)，B(3，0)关于原点的对称点分别为A′(1，0)，B(-3，0)．

　　 连结A′B′．

　　 则就可得到与线段AB关于原点对称的线段A′B′．

　　 例2．已知△ABC，A(1，2)，B(-1，3)，C(-2，4)利用关于原点对称的点的坐标的特点，作出△ABC关于原点对称的图形．

3．如图△ABO，绕点O旋转180°，画出旋转后的图形．

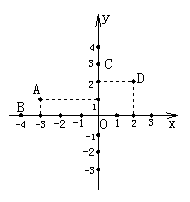
2．如图，△ABC是正三角形，以点A为中心，把△ADC顺时针旋转60°，画出旋转后的图形．

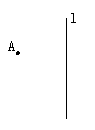
1．已知点A和直线L，如图，请画出点A关于L对称的点A′．

　　　　　　　　A　　　　　　　 B