⒈了解并会用直接开平方法和因式分解法解简单的一元二次方程。

　　 ⒉体会“降次转换”的基本思想，感受解一元二次方程中的转化美。

2、当方程出现相同因式(单项式或多项式)时，切不可约去相同因式，而应用因式分解法解。

[布置作业]：课本第37页习题1(5、6)、P38页习题2(1、2)

(1)(x+2)²=3(x+2)　　　　　　 (2)2y(y-3)=9-3y　　　　　　 (3)( x-2)² - x+2 =0

　(4)(2x+1)²=(x-1)²(5)。

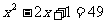练习：解下列方程

1)　　 2 (x+3)²=6(x+3)　 2)　 (2x+3⁾²=(4-2x)² 　　　3)　　 x(3x+1)=9x+3

[本课小结]：

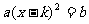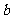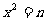1、对于形如(a≠0,a≥0)的方程，只要把看作一个整体，就可转化为(n≥0)的形式用直接开平方法解。

小张和小林一起解方程　　　　　　　 x(3x+2)－6(3x+2)＝0.

小张将方程左边分解因式，得

(3x+2)(x－6)＝0,

所以　 　　　　　 3x+2＝0,或x－6＝0.

方程的两个解为　　　　x₁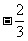＝，x₂＝6.

小林的解法是这样的：

移项，得　　　　　 　x(3x+2)＝6(3x+2),

方程两边都除以(3x+2)，得　　　　　 x＝6.

小林说:“我的方法多简便！”可另一个解x₁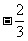＝哪里去了？

小林的解法对吗？你能解开这个谜吗？

学生先讨论交流，教师概括。

3、练习一 解下列方程：

(1)(x+2)²－16＝0； 　　　　　　(2)(x－1)²－18＝0；

(3)(1－3x)²＝1；　　　　　　　　 (4)(2x+3)²－25＝0.

2、说明：(1)这时，只要把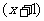看作一个整体，就可以转化为(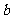≥0)型的方法去解决，这里体现了整体思想。

(2)　　　 在对方程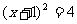两边同时开平方后，原方程就转化为两个一次方程。这种变形实质上是将原方程“降次”。“降次”也是一种重要的数学方法。

1、例1　 解下列方程

(1)(x+1)²－4＝0；　　　　　　　 (2)12(2－x)²－9＝0.

分　析　两个方程都可以转化为

²＝a

的形式，从而用直接开平方法求解.

解　(1)原方程可以变形为

(x+1)²＝4，

直接开平方，得

x+1＝±2.

所以原方程的解是　x₁＝1，x₂＝－3.

(1)　　　 原方程可以变形为

________________________，

有　　________________________.

所以原方程的解是　x₁＝________，x₂＝_________.

2、原方程可变形为

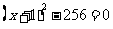
方程左边分解因式，得

(x+1+16)(x+1－16)=0

即可(x+17)(x－15)=0

所以x+17=0，x－15=0

原方程的蟹 x₁＝15，x₂＝－17

4、　　　　　　　 你是怎样解方程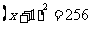的？

让学生说出作业中的解法，教师板书。

解：1、直接开平方，得x+1=±16

所以原方程的解是x₁＝15，x₂＝－17

3、　　　　　　　 你能解以下方程吗？

1)　　　　　　　 8－x²= -1　　 2)3y²-18=0　 3) x(x-1)+4x=0　　 4)-3x² -27=0