
3.用适当的方法解下列方程
(1)9(x-1)2=5 (2)x2+(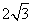 +1)x+
+1)x+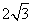 =0
=0 (3)(x+2)(x-5)=1
(3)(x+2)(x-5)=1
2.已知代数式x2+3x+5的值为9,求代数式3x2+9x-2的值。
㈠创设情境
⒈通过近几天的学习一元二次方程一般有哪几种解方法?通常你是如何选择的?和同学交流一下。
㈡自主学习
⒈用多种方法解下面方程,解完后讨论哪种方法较简便
(x+2)2+6(x+2)+9=0
㈢点拨矫正
⒈用适当的方法解下列方程
(1)(3x+1)2-(2x+1)2=0 (2)(x-2)(x+3)+4=0 (3)(x+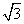 )2=4
)2=4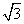 x
x
2. (1)已知y1=2x2+7x-1, y2=6x+2,当x取何值时,y1=y2
(2)如代数式x2+3x-9与代数式2x-5的值互为相反数求x的值.
㈣规律总结
一个一元二次方程只要有解原则上可以用四种解法分别来解,但实际操作中我们可根据方程的特点选择较为简便的方法。
㈤尝试练习
⒈填空
(1)已知(x2+y2)2-(x2+y2)=6则x2+y2的值为___________
(2) 在方程ax2+bx+c=0(a≠0)中若a+b+c=0则方程必有一根为___________;若a-b+c=0,则方程必有一根为_________。
⒈重点:能运用适当的方法解一元二次方程。
⒉难点:学习目标2
⒈能灵活应用直接开平方法,因式分解法,配方法及公式法解一元二次方程。
⒉能用联系和发展的眼光分析问题,树立转化的思想方法
㈠创设情境
⒈回顾上节课所学的两种方法。
⒉同学们能解下列方程吗?联想上节课所学的解法,你会怎么做呢?
⑴(x+3)2-2=0; ⑵4(x-1)2-9=0
㈡自主学习
⒈解下列方程:
⑴(x+2)2-9=0; ⑵15(4-x)2-5=0
⒉解方程:x(4x+2)-9(4x+2)=0
㈢点拨矫正
⒈解下列方程:
⑴(2x+3)2-25=0; ⑵4(x-1)2=9(x+2)2
⒉解下列方程:
⑴(x-2)2-x+2=0; ⑵(x-1)2-2(x2-1)=0
㈣规律总结
⒈
⒉
㈤尝试练习
⒈方程(x+2)2=4的根为( )
A、x1=-4,x2=-2 B、x1=-4,x2=0 C、x1=-4,x2=2 D、x1=0,x2=2
⒉方程x(x-1) (x+2)=0的根为( )
A、 x1=0,x2=1,x3=2 B、x1=-2,x2=1
C、x1=0,x2=1,x3=-2 D、x1=0,x2=-1,x3=2
⒊下列解题过程,正确的是( )
A、x2=-3,解x=±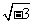 B、(x-1)2=9,解x-1=3,x=4
B、(x-1)2=9,解x-1=3,x=4
C、(x+3)2=4x,解x+3=±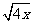 ,所以x=-3±2
,所以x=-3±2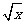
D、3(x-1)2=4,解(x-1)2=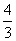 ,x-1=±
,x-1=±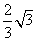 ,x=1±
,x=1±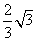
⒋方程(x-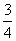 )2+(x-
)2+(x-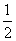 )(x-
)(x-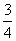 )=0的较小的根是( )
)=0的较小的根是( )
A、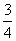 B、
B、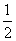 C、
C、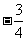 D、
D、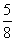
⒌解下列方程:
⑴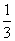 (2x+1)2=12; ⑵(
(2x+1)2=12; ⑵(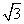 x+1)2-12=0
x+1)2-12=0
⒈重点: 灵活运用直接开平方法和因式分解法
⒉难点: 整体的数学思想
⒈能灵活运用直接开平方法和因式分解法解一元二次方程。
⒉了解整体的数学思想在解方程中的应用。
㈠创设情境
⒈判断下列方程是否为一元二次方程:⑴x2=16;⑵x2-81=0;并说出二次项系数、一次项系数和常数项。
⒉同学们会解上述方程吗?用你的方法和同学交流一下。
㈡自主学习
⒈试用两种方法解方程:x2-144=0
⒉解下列方程:⑴x2-18=0; ⑵81x2-16=0;
⒊解下列方程:⑴2x2+5x=0; ⑵8x2=16x;
㈢点拨矫正
⒈解下列方程:⑴2x2+5=0; ⑵3(x+2)2=27;
⒉解下列方程:⑴x(x-2)= 3(2-x); ⑵3(x+1) (x-2)=30;
㈣规律总结
⒈漏解:如方程x2=9、(x+1) 2=2(x+1)
⒉多解:如方程x2+9=0
⒊错解:如方程x2-2x-3=9
㈤尝试练习
⒈方程3x2-1=0的解为( )
A、x=±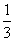 B、x=±
B、x=±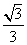 C、x=
C、x=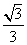 D、x=
D、x=
⒉方程x(x-2)= 3(2-x)的根为( )
A、x=4 B、x=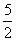 C、x1=
C、x1=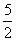 , x2=4 D、x1=
, x2=4 D、x1=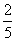 , x2=4
, x2=4
⒊请写出一个一元二次方程,使它的两个根为±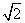 ,该方程可以是_______
,该方程可以是_______
⒋请写出一个根为x=1,另一个根满足-1<x<1的一元二次方程________
⒌解方程:⑴25x2-16=0; ⑵5x2-4x=0
⒈重点: 直接开平方法和因式分解法
⒉难点: “降次转换”的基本思想
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com