1、例1、解下列方程：

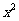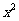(1)+2x＝5；　　　　　　 (2)－4x+3＝0.

思　考

能否经过适当变形，将它们转化为

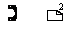　　 　　　　　　　= a　 的形式，应用直接开方法求解？

解(1)原方程化为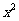+2x+1＝6， (方程两边同时加上1)

_____________________,　 _____________________,　 ____________________.

(2)原方程化为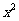－4x+4＝－3+4　　　　 (方程两边同时加上4)

_____________________,　 _____________________, _____________________.

归　纳　　 上面，我们把方程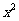－4x+3＝0变形为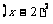＝1，它的左边是一个含有未知数的完全平方式，右边是一个非负常数.这样，就能应用直接开平方的方法求解.这种解一元二次方程的方法叫做配方法.

注意到第一步在方程两边同时加上了一个数后，左边可以用完全平方公式从而转化为用直接开平方法求解.

那么，在方程两边同时加上的这个数有什么规律呢？

例2、　　 用配方法解下列方程：

(1)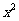－6x－7＝0；　　　　　 (2)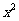+3x+1＝0.

2.引入新课

　我们知道，形如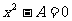的方程，可变形为，再根据平方根的意义，用直接开平方法求解．那么，我们能否将形如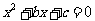的一类方程，化为上述形式求解呢？这正是我们这节课要解决的问题．

1.解下列方程，并说明解法的依据：

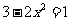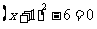　 (1)　　　　 (2)　　 (3)

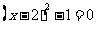
通过复习提问，指出这三个方程都可以转化为以下两个类型：

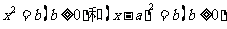
根据平方根的意义，均可用“直接开平方法”来解，如果b < 0，方程就没有实数解.

如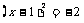请说出完全平方公式.

　 .

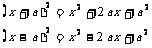2、当方程出现相同因式(单项式或多项式)时，切不可约去相同因式，而应用因式分解法解.

布置作业：课本第37页习题1(5、6)、P38页习题2(1、2)

教学反思：

(老师先引导学生小结，再进行总结)

1、对于形如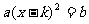(a≠0,a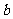≥0)的方程，只要把看作一个整体，就可转化为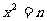(n≥0)的形式用直接开平方法解.

(1)(x+2)²－16＝0；　　　　　　 (2)(x－1)²－18＝0；

(3)(1－3x)²＝1；　　　　　　　　 (4)(2x+3)²－25＝0.

　　　　　　　 练习二：解下列方程

(1)(x+2)²=3(x+2)　　　　　 (2)2y(y-3)=9-3y　　　　　　 (3)( x-2)² - x+2 =0

(4)(2x+1)²=(x-1)² 　　　　　(5).

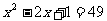2、说明：(1)这时，只要把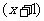看作一个整体，就可以转化为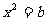(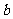≥0)型的方法去解决，这里体现了整体思想.

1、例1　 解下列方程

(1)(x+1)²－4＝0；　　　　　　　 (2)12(2－x)²－9＝0.

分　析　两个方程都可以转化为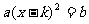(a≠0,ab≥0)

的形式，从而用直接开平方法求解.

解　(1)原方程可以变形为

(x+1)²＝4，

直接开平方，得：x+1＝±2.　 所以原方程的解是　x₁＝1，x₂＝－3.

原方程可以变形为________________________，

有________________________.

所以原方程的解是　x₁＝________，x₂＝_________.

问：怎样解方程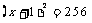的？让学生说出作业中的解法，教师板书.

解：1.直接开平方，得x+1=±16

所以原方程的解是x1＝15，x2＝－17

2.原方程可变形为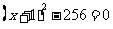

方程左边分解因式，得(x+1+16)(x+1－16)=0即可(x+17)(x－15)=0

所以x+17=0，x－15=0　 原方程的解为： x₁＝15，x₂＝－17