
2、现在,你能解决§23.1的问题1了吗?
1、用多种方法解方程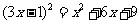
让学生尝试用多种方法解方程,归结为:
解法1:将方程化为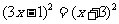 ,直接开平方,得
,直接开平方,得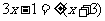
解得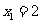 ,
,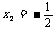 .
.
解法2:将方程化为一般形式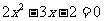 ,进而转化为
,进而转化为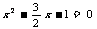 ,用配方法可求方程的解.
,用配方法可求方程的解.
解法3:将方程化为一般形式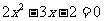 ,用公式法求解,其中
,用公式法求解,其中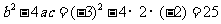 .
.
提问:用哪种方法解方程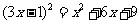 更简便?
更简便?
根据你学习的体会,小结一下解一元二次方程一般有哪几种方法?通常你是如何选择的?和同学交流一下.
作业设计:
P38习题4.(3)、(4)、(5)、(6)、(7)、(8),5.
教学反思:
3、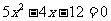 ; 4、
; 4、
教学要点:(1)对于方程(2)和(4),首先要把方程化为一般形式;
(2)强调确定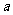 、
、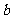 、
、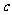 值时,不要把它们的符号弄错;
值时,不要把它们的符号弄错;
(3)先计算 的值,再代入公式.
的值,再代入公式.
例2、(补充)解方程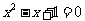
解:这里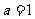 ,
,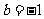 ,
,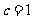 ,
,
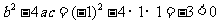
因为负数不能开平方,所以原方程无实数根.
让学生反思以上解题过程,归纳得出:
当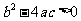 时,方程有两个不相等的实数根;
时,方程有两个不相等的实数根;
当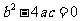 时,方程有两个相等的实数根;
时,方程有两个相等的实数根;
当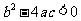 时,方程没有实数根.
时,方程没有实数根.
1、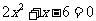 ; 2、
; 2、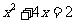 ;
;
问题1:能否用配方法把一般形式的一元二次方程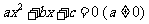 转化为
转化为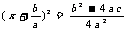 呢?教师引导学生回顾用配方法解数字系数的一元二次方程的过程,让学生分组讨论交流,达成共识:
呢?教师引导学生回顾用配方法解数字系数的一元二次方程的过程,让学生分组讨论交流,达成共识:
因为 ,方程两边都除以
,方程两边都除以 ,得
,得
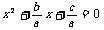 移项,得
移项,得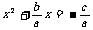 配方,得
配方,得
 即
即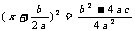
问题2:当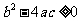 ,且
,且 时,
时, 大于等于零吗?
大于等于零吗?
让学生思考、分析,发表意见,得出结论:当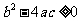 时,因为
时,因为 ,所以
,所以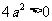 ,从而
,从而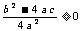 .
.
问题3:在研究问题1和问题2中,你能得出什么结论?
让学生讨论、交流,从中得出结论,当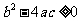 时,一般形式的一元二次方程
时,一般形式的一元二次方程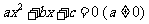 的根为
的根为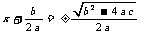 ,即
,即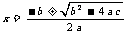 . 由以上研究的结果,得到了一元二次方程
. 由以上研究的结果,得到了一元二次方程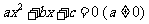 的求根公式:
的求根公式: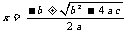 (
(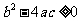 )
)
这个公式说明方程的根是由方程的系数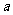 、
、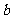 、
、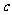 所确定的,利用这个公式,我们可以由一元二次方程中系数
所确定的,利用这个公式,我们可以由一元二次方程中系数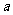 、
、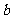 、
、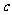 的值,直接求得方程的解,这种解方程的方法叫做公式法.
的值,直接求得方程的解,这种解方程的方法叫做公式法.
思考:当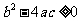 时,方程有实数根吗?
时,方程有实数根吗?
3、用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一种更好的方法,迅速求得一元二次方程的实数根呢?
2、用配方解一元二次方程的步骤是什么?
1、用配方法解下列方程:
(1) (2)
(2)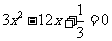
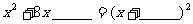 ;
; 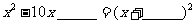
 ;
; 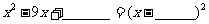
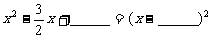 ;
;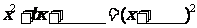
通过练习,使学生认识到:配方的关键是在方程两边同时添加的常数项等于一次项系数一半的平方.
2、练习:
①.填空:
(1)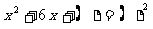 (2)
(2)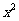 -8x+( )=(x- )2
-8x+( )=(x- )2
(3)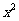 +x+( )=(x+
)2; (4)4
+x+( )=(x+
)2; (4)4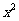 -6x+( )=4(x- )2
-6x+( )=4(x- )2
② 用配方法解方程:
(1)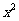 +8x-2=0 (2)
+8x-2=0 (2)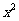 -5 x-6=0. (3)
-5 x-6=0. (3)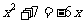
本课小结: 本节你学到了什么知识?有什么收获?(老师先引导学生小结,再进行总结) 配方法解一元二次方程的步骤:1、把常数项移到方程右边,用二次项系数除方程的两边使新方程的二次项系数为1;2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;
如果方程的右边整理后是非负数,用直接开平方法解之,如果右边是个负数,则指出原方程无实根.
布置作业:P38页习题2.(3)、(4)、(5)、(6),3,4.(1)、(2)
教学反思:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com