(学生活动)请同学们独立完成下面的各题．

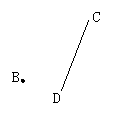
1．如图，已知线段CD是线段AB平移后的图形，D是B点的对称点，作出线段AB，并回答，AB与CD有什么位置关系．

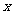　　 关于量的变化率问题，不管是增加还是减少，都是变化前的数据为基础，每次按相同的百分数变化，若原始数据为，设平均变化率为，经第一次变化后数据为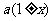；经第二次变化后数据为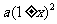.在依题意列出方程并解得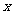值后，还要依据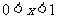的条件，做符合题意的解答.

作业设计：　 P38 习题8、9

教学反思：

　　 某药品两次升价，零售价升为原来的 1.2倍，已知两次升价的百分率一样，求每次升价的百分率(精确到0.1%)

解，设原价为元，每次升价的百分率为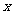，根据题意，得

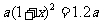解这个方程，得

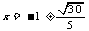由于升价的百分率不可能是负数，所以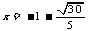不符合题意，因此符合题意要求的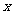为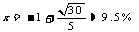

答：每次升价的百分率为9.5%.

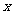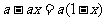　　 分析：“两次降价的百分率一样”，指的是第一次和第二次降价的百分数是一个相同的值，即两次按同样的百分数减少，而减少的绝对数是不相同的，设每次降价的百分率为，若原价为，则第一次降价后的零售价为，又以这个价格为基础，再算第二次降价后的零售价.

　　 思考：原价和现在的价格没有具体数字，如何列方程？请同学们联系已有的知识讨论、交流.

　　 解　设原价为1个单位，每次降价的百分率为x.根据题意，得

(1－x) ²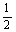＝ 解这个方程，得x＝

由于降价的百分率不可能大于1，所以x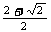＝不符合题意，因此符合本题要求的x为

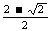≈29.3%.

答：每次降价的百分率为29.3%.

　　 百分数的概念在生活中常常见到，而量的变化率更是经济活动中经常接触，下面，我们就来研究这样的问题.

问题：某商品经两次降价，零售价降为原来的一半，已知两次降价的百分率一样.求每次降价的百分率.(精确到0.1%)

　　 让学生反思、归纳、总结，应用一元二次方程解实际问题，要认真审题，要分析题意，找出数量关系，列出方程，把实际问题转化为数学问题来解决.求得方程的解之后，要注意检验是否任命题意，然后得到原问题的解答.

作业设计：P38　 习题5、6、7

教学反思：

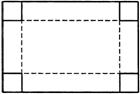
　　 如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方米.求截去正方形的边长.

解：设截去正方形的边长x厘米，底面(图中虚线线部分)长等于　　　　 　　厘米，宽等于 　　　　　　　厘米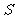，底面= 　　　　　　　.

请同学们自己列出方程并解这个方程，讨论它的解是否符合题意.

由学生回答解题过程，教师板书：

解　设截去正方形的边长为x厘米，根据题意，得

(60－2x) (40－2x) ＝800

解方程得

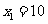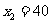，，经检验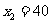，不符合题意，应舍去，符合题意的解是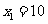

答：截去正方形的边长为10厘米.

3.1和2说明了什么问题？

让学生交流讨论、体会到把实际问题转化为数学问题来解决，求得方程的解，不一定是原问题的解答，因此，要注意是检验解是否符合题意.

作为应用题，还应作答.

2、所求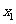、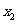都符合题意吗？

让学生思考、分析，真正理解负数根不符合题意，应舍去符合题意的解是：

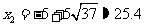
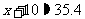
　　 请同学们先看看P26页问题1，要想解决§23.1的问题1，首先要解方程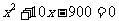，同学们能解这个方程吗？

让学生动手解题并口答结果：,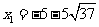

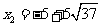
提问：

1、所求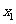、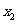都是所列方程的解吗？