
1.B 2.D 3.B 4.C 5.D 6.B 7.C 8.A 9.D 10.D
26.(改编)(8分)如图,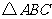 是⊙O的内接三角形,
是⊙O的内接三角形,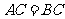 ,
,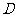 为⊙O中⌒AB上一点,延长
为⊙O中⌒AB上一点,延长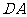 至点
至点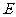 ,使
,使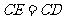 .
.
(1)求证: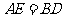 ;
;
(2)若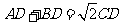 ,求证:
,求证:
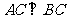 .
.
圆24.1.1-1.4综合训练
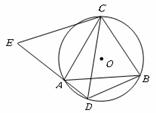
25.(8分)如图,⊙O是△ABC的外接圆,AB为直径,⌒AC=⌒CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求∠ACB的度数;
(2)求证:AE=CE;
答案:证明:(1)∵AB为⊙O的直径,∴∠ACB=90°.
(2)∵AB为直径,且AB⊥CG,∴AC=AG .
又∵⌒AC=⌒CF,∴AG=CF,∴∠ACG=∠CAF,∴AE=CE.
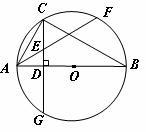
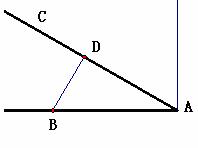
24.(6分)如图.某货船以20海里∕时的速度将一批重要物资由A处运往正西方向的B 处,经16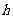 的航行达到,达到后必须立即卸货。此时接到气象部门的通知,一台风中心正以40海里∕时的速度由A向北偏西
的航行达到,达到后必须立即卸货。此时接到气象部门的通知,一台风中心正以40海里∕时的速度由A向北偏西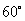 的方向移动,距台风中心200海里的圆形区域(包括边界)均回受到影响。问:
的方向移动,距台风中心200海里的圆形区域(包括边界)均回受到影响。问:
(1).B处是否回受到台风的影响?请说明理由:
(2).为避免受到台风的影响,该船应在多少小时内卸完货物? (供选用数据:
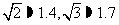 )
)
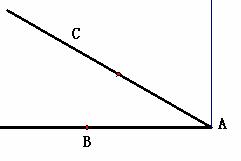
答案:解:(1)过点B作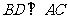 于D,
于D,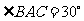 ,在
,在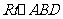 中,
中,
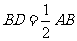
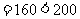 ,所以,B处会受到台风的影响。
,所以,B处会受到台风的影响。
(2)以点B为圆心,200海里为半径画圆,交AC于E、F,则有:DF=DE=120,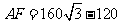 ,所以
,所以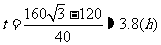 ,因此,该船应在3.8小时内卸完货物。
,因此,该船应在3.8小时内卸完货物。

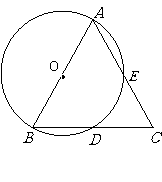
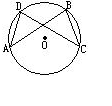
23.(6分)如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,ΔABC还需满足什么条件,点E才一定是AC的中点?(直接写出结论)

答案:解:(1)AB=AC.
连结AD,则AD⊥BC.
又BD=DC,∴ AD是线段BD的中垂线.
∴ AB=AC.
(2) △ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C
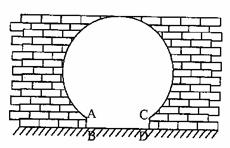
22.(5分)(2008黄冈市)如图是“明清影视城”的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据,于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20 cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少?
答案:证明:过O作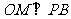 于M,
于M,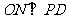 于N
于N
∵OP∠EPF ∴OM=ON,PM=PN,∴AB=CD,则BM=DN,∴PM+BM=PN+ND,∴PB=PD
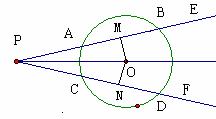
21.(5分)如图,已知:⊙O的半径为5,弦AB长为8,弦BC∥OA,求AC长
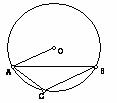
答案: 解:延长AO交⊙与D,连结BD,∴∠ABD=90°,由勾股定理可得BD=6,∵BC∥OA,∴∠DAB=ABC, ∴ AC=BD=6
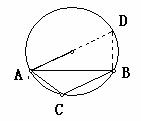
20.(5分)如图,AD、BC是⊙O的两条弦,且AD=BC,
求证:AB=CD。

答案:证明:∵AD=BC,∴AD=BC,∴AD+BD=BC+BD,即AB=CD,∴AB=CD。
19.(5分) 如图,已知: AB交圆O于C、D,且 AC=BD.你认为OA=OB吗?为什么?
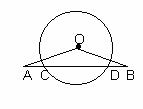
答案:证明:过点O作 于E
于E
 ∴AE=BE ∴AO=BO(三线合一)
∴AE=BE ∴AO=BO(三线合一)
18.半径为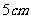 的圆O中有一点P,OP=4,则过P的最短弦长_________,最长弦是__________,
的圆O中有一点P,OP=4,则过P的最短弦长_________,最长弦是__________,
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com