
4.如图5,已知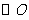 中,
中,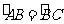 ,且
,且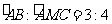 ,则
,则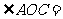 ______.
______.
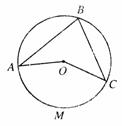
3.(山东滨州)如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( )
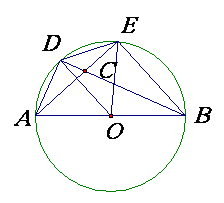
A、2个 B、3个 C、4个 D、5个
答案:C
2. 在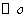 中,
中,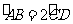 ,那么( )
,那么( )
A. 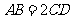
B.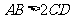
C.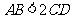
D.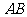 与
与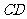 的大小关系不定。
的大小关系不定。
1.下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③ 相等的圆心角所对的弧相等.④在同圆或等圆中,如果两条弧相等,那么弦也相等。其中真命题的是( )
A.①② B. ②④ C. ①②④ D. ①②③
答案:A
26.答案:证明:(1)在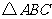 中,
中,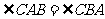 .
.
在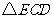 中,
中,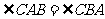 .
.
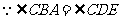 ,(同弧上的圆周角相等)
,(同弧上的圆周角相等)
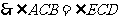 .
.
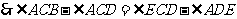 .
.
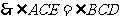 .
.
在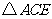 和
和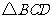 中,
中,
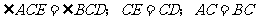
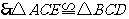 .
.
 .
.
(2)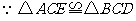 ,∴ EA=BD, 若
,∴ EA=BD, 若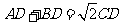
∴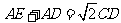 ,即
,即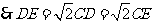 .
.
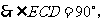 ∴
∴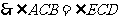 =90°
=90°
又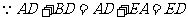 ∴
∴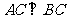
答案:证明:(1)在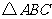 中,
中,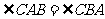 .
.
在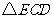 中,
中,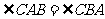 .
.
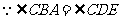 ,(同弧上的圆周角相等)
,(同弧上的圆周角相等)
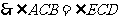 .
.
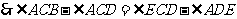 .
.
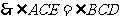 .
.
在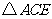 和
和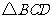 中,
中,
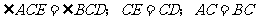
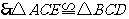 .
.
 .
.
(2)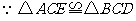 ,∴ EA=BD, 若
,∴ EA=BD, 若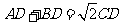
∴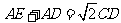 ,即
,即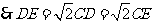 .
.
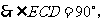 ∴
∴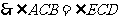 =90°
=90°
又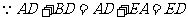 ∴
∴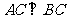
25.证明:(1)∵AB为⊙O的直径,∴∠ACB=90°.
(2)∵AB为直径,且AB⊥CG,∴AC=AG .
又∵⌒AC=⌒CF,∴AG=CF,∴∠ACG=∠CAF,∴AE=CE.
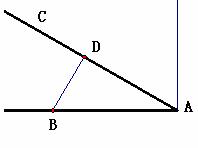
24.解:(1)过点B作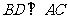 于D,
于D,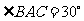 ,在
,在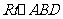 中,
中,
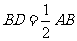
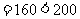 ,所以,B处会受到台风的影响。
,所以,B处会受到台风的影响。
(2)以点B为圆心,200海里为半径画圆,交AC于E、F,则有:DF=DE=120,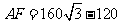 ,所以
,所以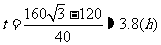 ,因此,该船应在3.8小时内卸完货物。
,因此,该船应在3.8小时内卸完货物。

23.解:(1)AB=AC.
连结AD,则AD⊥BC.
又BD=DC,∴ AD是线段BD的中垂线.
∴ AB=AC.
(2) △ABC为正三角形,或AB=BC,或AC=BC,或∠A=∠B,或∠A=∠C
22.证明:过O作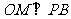 于M,
于M,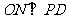 于N
于N
∵OP∠EPF ∴OM=ON,PM=PN,∴AB=CD,则BM=DN,∴PM+BM=PN+ND,∴PB=PD
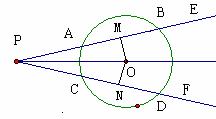
21.解:,连接AC,作AC的中垂线交AC于G,交BD于N,交圆的另一点为M,由垂径定理可知:MN为圆弧形的所在的圆与地面的切点,取MN的中点O,则O为圆心,连接OA、OC,
∵AB⊥BD,CD⊥BD,
∴AB∥CD.
∵AB=CD,
∴四边形ABCD为矩形,
∴AC=BD=200cm,GN=AB=CD=20 cm,
∴AG=GC=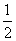 AC=100 cm.
AC=100 cm.
设⊙O的圆心为R,由勾股定理得
OA2=OG2+AG2,即R2=(R-20)2+1002,
解得R=260 cm,
∴MN=2R=520 cm.
答:这个圆弧形门的最高点离地面的高度是=520 cm.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com