
4.选用课时作业设计.
第一课时作业设计
3.垂径定理推论的证明.
2.车轮为什么是圆的呢?
1.教材P94 复习巩固1、2、3.
3.垂径定理及其推论以及它们的应用.
2.圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
本节课应掌握:
1.圆的有关概念;
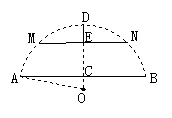
例2.有一石拱桥的桥拱是圆弧形,如图24-5所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面宽MN=32m时是否需要采取紧急措施?请说明理由.
分析:要求当洪水到来时,水面宽MN=32m是否需要采取紧急措施,只要求出DE的长,因此只要求半径R,然后运用几何代数解求R.
 解:不需要采取紧急措施
解:不需要采取紧急措施
设OA=R,在Rt△AOC中,AC=30,CD=18
R2=302+(R-18)2 R2=900+R2-36R+324
解得R=34(m)
连接OM,设DE=x,在Rt△MOE中,ME=16
342=162+(34-x)2
162+342-68x+x2=342 x2-68x+256=0
解得x1=4,x2=64(不合设)
∴DE=4
∴不需采取紧急措施.
教材P86 练习 P88 练习.
3.我是利用沿着圆的任意一条直径折叠的方法解决圆的对称轴问题的.
因此,我们可以得到:
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
(学生活动)请同学按下面要求完成下题:
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
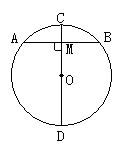
(1)如图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你理由.
(老师点评)(1)是轴对称图形,其对称轴是CD.
(2)AM=BM,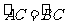 ,
,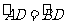 ,即直径CD平分弦AB,并且平分
,即直径CD平分弦AB,并且平分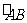 及
及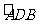 .
.
这样,我们就得到下面的定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
下面我们用逻辑思维给它证明一下:
已知:直径CD、弦AB且CD⊥AB垂足为M
求证:AM=BM,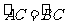 ,
,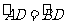 .
.
分析:要证AM=BM,只要证AM、BM构成的两个三角形全等.因此,只要连结OA、OB或AC、BC即可.
证明:如图,连结OA、OB,则OA=OB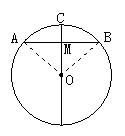
在Rt△OAM和Rt△OBM中
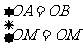
∴Rt△OAM≌Rt△OBM
∴AM=BM
∴点A和点B关于CD对称
∵⊙O关于直径CD对称
∴当圆沿着直线CD对折时,点A与点B重合, 与
与 重合,
重合,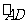 与
与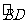 重合.
重合.
∴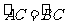 ,
,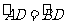
进一步,我们还可以得到结论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
(本题的证明作为课后练习)
例1.如图,一条公路的转弯处是一段圆弦(即图中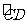 ,点O是
,点O是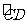 的圆心,其中CD=600m,E为
的圆心,其中CD=600m,E为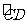 上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
分析:例1是垂径定理的应用,解题过程中使用了列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.
解:如图,连接OC
 设弯路的半径为R,则OF=(R-90)m
设弯路的半径为R,则OF=(R-90)m
∵OE⊥CD
∴CF=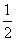 CD=
CD=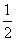 ×600=300(m)
×600=300(m)
根据勾股定理,得:OC2=CF2+OF2
即R2=3002+(R-90)2 解得R=545
∴这段弯路的半径为545m.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com