本堂课我们探索了直线与圆的位置关系，有几种？是如何来判断的？

直线与圆有三种位置关系，分别是相离、相切、相交：

(1)如果一条直线与一个圆没有公共点，那么就说这条直线与这个圆相离；

(2)如果一条直线与一个圆只有一个公共点，那么就说这条直线与这个圆相切．此时这条直线叫做圆的切线，这个公共点叫做切点；

(3)如果一条直线与一个圆有两个公共点，那么就说这条直线与这个圆相交．此时这条直线叫做圆的割线．

我们用圆心与直线的距离与半径的大小关系来判断直线与圆的位置关系．设⊙O的半径为r，圆心O到直线l的距离为d，则：

(1)d＞r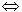直线与圆相离；

(2)d＝r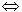直线与圆相切；

(3)d＜r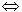直线与圆相交．　

例1 在△ABC中，AB＝10cm，BC＝6cm，AC＝8cm，(1)若以C为圆心，4 cm长为半径画⊙C，则⊙C与AB的位置关系怎样？(2)若要使AB与⊙C 相切，则⊙C的半径应当是多少？(3)若要以AC为直径画⊙O，则⊙O与AB、BC的位置关系分别怎样？

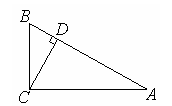
分析 判断⊙C与AB的位置关系应求出点C到AB的距离CD的长，然后再与半径作比较，即可求出⊙C与AB的位置关系．而要求CD的长，可利用　△ABC的面积，但应首先　判断　△ABC　为直角三角形．　

解 过C作CD⊥AB，垂足为D　．　　　　　

因为BC²+AC²＝6²+8²＝100，AB²＝10²＝100，

所以BC²+AC²＝ AB²，故△ABC是直角三角形，根据三角形面积相等得：

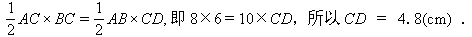
(1)若以C为圆心，4cm长为半径画⊙C ，因为4cm＜4.8cm，所以⊙C与AB的位置关系为相离．

(2)若要使AB与⊙C相切，则⊙C的半径应为4.8cm ．

(3)若以AC为直径画⊙O，由于BC⊥AC，故⊙O与BC相切；⊙O与AB相交．

例2 在Rt△ABC中，∠C＝90°，O是BC的中点，以O为圆心的圆与线段AB有两个交点，若AC＝3，BC＝4，求半径r的取值范围．

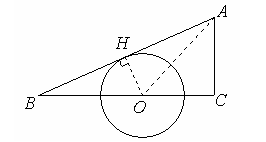
分析 过O作OH⊥AB，根据△ABC∽△BOH求出OH，即可求出半径r的范围．

解 过O作OH⊥AB，垂足为H，又∠C＝90°，所以Rt△ABC∽Rt△BOH，

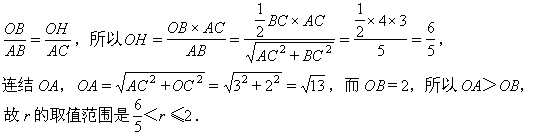
例3 如图，△ABO中，OC⊥AB于C，∠AOC＝∠B，AC＝16cm，BC＝4cm，⊙O的半径为8cm，AB是⊙O的切线吗？试说明．

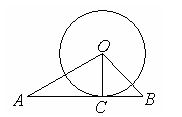
分析 根据直线与圆的位置关系可知，要得到AB是⊙O的切线，只需求出OC＝8cm．

解 因为OC⊥AB，∠AOC＝∠B，Rt△AOC∽Rt△OBC，

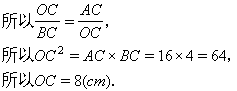
又因为⊙O的半径为8cm，所以AB是⊙O的切线．

我们再来做一个实验，在纸片上画一条直线，把硬币的边缘看作圆，在纸上移动硬币，你能发现直线与圆的公共点个数的变化情况吗？公共点个数最少时有几个？最多时有几个？请做完实验后把你的发现互相交流一下，把结论告诉老师？

在实验中我们看到，直线与圆的公共点最少时没有，最多时有两个，在移动过程中发现直线与圆的公共点有时只有一个，即直线与圆的位置关系有下面的三种情形．

如上图(1)，如果一条直线与一个圆没有公共点，那么就说这条直线与这个圆相离．

如上图(2)，如果一条直线与一个圆只有一个公共点，那么就说这条直线与这个圆相切．此时这条直线叫做圆的切线，这个公共点叫做切点．

如上图(3)，如果一条直线与一个圆有两个公共点，那么就说这条直线与这个圆相交．此时这条直线叫做圆的割线．

直线与圆的位置关系只有三种：相离、相切、相交．那么能否用数量关系来表示直线与圆的位置关系呢？

从前面的图中已发现，设如上图(2)，如果一条直线与一个圆只有一个公共点，那么就说这条直线与这个圆相切．此时这条直线叫做圆的切线，这个公共点叫做切点．⊙O的半径为r，圆心到直线的距离为d，我们也可用d和r之间的大小关系来判断直线与圆的位置关系．

当时，如上图(1)圆心O到直线l的距离d大于半径r，因而直线上的所有点到圆心的距离都大于半径r，说明直线l在圆的外部，与圆没有公共点，因此当d＞r时，直线与圆的位置关系是相离，反之，如果已知直线l与⊙O相离，则d＞r．即： d＞r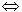直线与圆相离．

同理可知，d＝r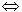直线与圆相切．d＜r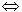直线与圆相交．　

我们都知道，点和圆的位置关系有三种：点在圆内、点在圆上、点在圆外．那么直线和圆的位置关系又怎样呢？

大家也许看过日出，如果我们把太阳看作一个圆，那么太阳在升起的过程中，和地平线的关系就体现了直线和圆的几种位置关系．

4、在探索垂径定理的过程中，对部分学生来说存在着困难，因此，教师在教学过程中除了是组织者和引导者之外，还应扮演“伯乐”和“雷锋”的角色，多给学生一些赞许鼓励和帮助，让更多的学生参与到学习中来．

3．通过实例了解了古代人的智慧，体会垂径定理的文化价值，使学生热爱科学，热爱探索，并树立远大的理想．

2．在探索垂径定理的过程中，增强了同学们的猜测、推理等技巧，并且考查了学生分析问题的能力，动手与思考的有机结合，对学生思考问题和解决问题都有很大的帮助．

1．《数学课程标准》指出：“本学段(7-9年级)的数学应结合具体的数学内容，采用‘问题情境--建立模型--解释、应用与拓展’的模式展开，让学生经历知识的形成与应用的过程…… ”因此，在本节课的教学中，我不断的创造自主探究与合作交流的学习环境，让学生有充分的时间和空间去动手操作，去观察分析，去得出结论，并体验成功，共享成功．

(六)布置作业，应用新知

考虑的学生的个体差异，我设计了必做题和选做题，让更多的同学参与到数学中来．