教材P100　 练习1、2、3、4．

　　 由上面的画图以及所学知识，我们可知：

　　 设⊙O的半径为r，点P到圆心的距离为OP=d

　　 则有：点P在圆外d>r

　　 点P在圆上d=r

　　 点P在圆内d<r

　　 反过来，也十分明显，如果d>r点P在圆外；如果d=r点P在圆上；如果d<r点P在圆内．

　　 因此，我们可以得到：

这个结论的出现，对于我们今后解题、判定点P是否在圆外、圆上、圆内提供了依据．

　　 下面，我们接下去研究确定圆的条件：

　　 (学生活动)经过一点可以作无数条直线，经过二点只能作一条直线，那么，经过一点能作几个圆？经过二点、三点呢？请同学们按下面要求作圆．

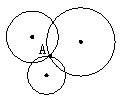
　　 (1)作圆，使该圆经过已知点A，你能作出几个这样的圆？

　　 (2)作圆，使该圆经过已知点A、B，你是如何做的？你能作出几个这样的圆？其圆心的分布有什么特点？与线段AB有什么关系？为什么？

　　 (3)作圆，使该圆经过已知点A、B、C三点(其中A、B、C三点不在同一直线上)，你是如何做的？你能作出几个这样的圆？

　　 老师在黑板上演示：

(1)无数多个圆，如图1所示．

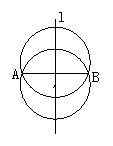
　　 (2)连结A、B，作AB的垂直平分线，则垂直平分线上的点到A、B的距离都相等，都满足条件，作出无数个．

其圆心分布在AB的中垂线上，与线段AB互相垂直，如图2所示．

　　　　　 (1)　　　　　　　　　　 (2)　　　　　　　　　　　 (3)

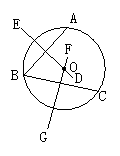
　　 (3)作法：①连接AB、BC；

　　 ②分别作线段AB、BC的中垂线DE和FG，DE与FG相交于点O；

③以O为圆心，以OA为半径作圆，⊙O就是所要求作的圆，如图3所示．

在上面的作图过程中，因为直线DE与FG只有一个交点O，并且点O到A、B、C三个点的距离相等(中垂线上的任一点到两边的距离相等)，所以经过A、B、C三点可以作一个圆，并且只能作一个圆．

　　 即：不在同一直线上的三个点确定一个圆．

　　 也就是，经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆．

　　 外接圆的圆心是三角形三条边垂直平分线的交点，叫做这个三角形的外心．

　　 下面我们来证明：经过同一条直线上的三个点不能作出一个圆．

证明：如图，假设过同一直线L上的A、B、C三点可以作一个圆，设这个圆的圆心为P，那么点P既在线段AB的垂直平分线L₁，又在线段BC的垂直平分线L₂，即点P为L₁与L₂点，而L₁⊥L，L₂⊥L，这与我们以前所学的“过一点有且只有一条直线与已知直线垂直”矛盾．

所以，过同一直线上的三点不能作圆．

　　 上面的证明方法与我们前面所学的证明方法思路不同，它不是直接从命题的已知得出结论，而是假设命题的结论不成立(即假设过同一直线上的三点可以作一个圆)，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到命题成立．这种证明方法叫做反证法．

　　 在某些情景下，反证法是很有效的证明方法．

　　 例1．某地出土一明代残破圆形瓷盘，如图所示．为复制该瓷盘确定其圆心和半径，请在图中用直尺和圆规画出瓷盘的圆心．

　　 分析：圆心是一个点，一个点可以由两条直线交点而成，因此，只要在残缺的圆盘上任取两条线段，作线段的中垂线，交点就是我们所求的圆心．

　　 作法：(1)在残缺的圆盘上任取三点连结成两条线段；

　　 (2)作两线段的中垂线，相交于一点．

　　 则O就为所求的圆心．

4．如果在圆外有一点呢？圆内呢？请你画图想一想．

　　 老师点评：(1)在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆；圆心为O，半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形．

　　 (2)圆规：一个定点，一个定长画圆．

　　 (3)都等于半径．

　　 (4)经过画图可知，圆外的点到圆心的距离大于半径；圆内的点到圆心的距离小于半径．

3．圆形成后圆上这些点到圆心的距离如何？

2．你能至少举例两个说明圆是如何形成的？

　　 (学生活动)请同学们口答下面的问题．

1．圆的两种定义是什么？

4.已知⊙O的半径为5厘米，弦AB＝8cm，以3.5cm为半径作一个同心圆，则所作的圆与弦AB的位置关系如何？

3.如果⊙O的直径为10厘米，圆心O到直线AB的距离为10厘米，那么⊙O与直线AB有怎样的位置关系？

2.已知圆的半径等于10厘米，直线l和圆只有一个公共点，求圆心到直线l的距离．

1.已知圆的半径等于5厘米，圆心到直线l的距离是：(1)4厘米；(2)5厘米；(3)6厘米．直线l与圆分别有几个公共点？分别说出直线l与圆的位置关系？