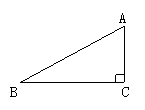
2．如图，Rt△ABC，∠C=90°，AC=3cm，BC=4cm，则它的外心与顶点C的距离为(　 )．

A．2.5　　　 B．2.5cm　　 C．3cm　　 D．4cm

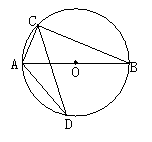
1．下列说法：①三点确定一个圆；②三角形有且只有一个外接圆；③圆有且只有一个内接三角形；④三角形的外心是各边垂直平分线的交点；⑤三角形的外心到三角形三边的距离相等；⑥等腰三角形的外心一定在这个三角形内，其中正确的个数有( )

　　　 A．1 　　　B．2　　　 C．3　　　 D．4

2．选用课时作业设计．

第一课时作业设计

1．教材P110　 复习巩固　 1、2、3．

5．以上内容的应用．

4．反证法的证明思想．

3．三角形外接圆和三角形外心的概念．

2．不在同一直线上的三个点确定一个圆．

　　 本节课应掌握：

1．　 点和圆的位置关系：设⊙O的半径为r，点P到圆心的距离为d，则

例2．如图，已知梯形ABCD中，AB∥CD，AD=BC，AB=48cm，CD=30cm，高27cm，求作一个圆经过A、B、C、D四点，写出作法并求出这圆的半径(比例尺1：10)

　　 分析：要求作一个圆经过A、B、C、D四个点，应该先选三个点确定一个圆，然后证明第四点也在圆上即可．要求半径就是求OC或OA或OB，因此，要在直角三角形中进行，不妨设在Rt△EOC中，设OF=x，则OE=27-x由OC=OB便可列出，这种方法是几何代数解．

　　 作法分别作DC、AD的中垂线L、m，则交点O为所求△ADC的外接圆圆心．

　　 ∵ABCD为等腰梯形，L为其对称轴

　　 ∵OB=OA，∴点B也在⊙O上

　 　∴⊙O为等腰梯形ABCD的外接圆

　　 设OE=x，则OF=27-x，∵OC=OB

　　 ∴

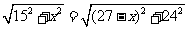
　　 解得：x=20

　　 ∴OC==25，即半径为25m．