
学习了两圆的公切线,应该掌握以下几个方面;(让学生自己总结,并全班交流).
1.由圆的轴对称性,两圆外(或内)公切线的交点(如果存在)在连心线上.
例4 教材P.144如图7-110,⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点.
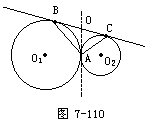
求证:AB⊥AC.
分析:题目中已知⊙O1和⊙2外切于点A.这是一个非常特殊的点,过点A我们引两圆的内公切线,产生了三种可能:①运用弦切角定理.②切线的性质定理.③切线长定理.在一道关于两圆相切的问题中,作出公切线后,还要针对已知条件,选择之,本例中已知两圆的外公切线BC,所以过点A的内公切线与之相交,必然产生切线长定理运用的前提,使问题得证.
证明:过点A作⊙O1和⊙O2的内公切线交BC于点O.

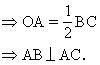
练习一,P.145中2如图7-111,⊙O1和⊙O2相切于点T,直线AB、CD经过点T,交⊙O1于点A、C,交⊙O2于点B、D,求证:AC∥BD.
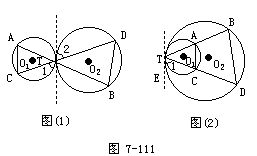
分析:欲证AC∥BD,须证∠A=∠B,图(1)中∠A和∠B是内错角,图(2)中∠A和∠B是同位角.而∠A和∠B从图形中的位置看是两个圆中的圆周角,必须存在第三个角,使∠A和∠B都与之相等,从而∠A和∠B相等.
证明:过点T作两圆的内公切线TE.
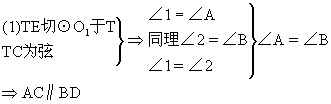
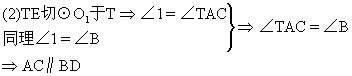
练习二,P.153中14 已知:⊙O和⊙O′外切于点A,经过点A作直线BC和DE,BC交⊙O于点B,交⊙O′于点C,DE交⊙O于点D,交⊙O′于E,∠BAD=40°,∠ABD=70°,求∠AEC的度数.

分析:已知⊙O中的圆周角求⊙O′中的圆周角,而两圆外切,作内公切线即可.
解:过点A作⊙O和⊙O′的内公切线AF.
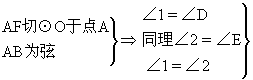
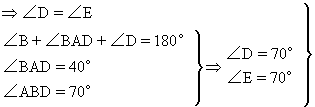
练习三,P.153中15.经过相内切的两圆的切点A作大圆的弦AD、AE,设AD、AE分别和小圆相交于B、C.
求证:P.153中AB∶AC=AD∶AE.
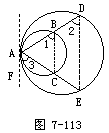
分析:证比例线段,一是三角形相似,二是平行线.由题设两圆相切,可作出切线,证平行线所成比例线段.
证明:连结BC、DE.过点A作两圆的公切线AF.
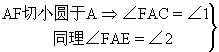
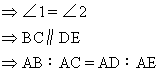
我们已经学习了圆的切线在几何证明中的重要作用,这节课,我们来学习两圆公切线在证明中的作用.
实际上两圆的公切线,对两圆起着一个桥梁的作用,首先,对于每一个圆,公切线都会产生切线的性质.另外公切线和过切点的两圆的弦,会产生弦切角定理运用的前提,从而把两个圆中的圆周角建立相等关系,我们有下面的例子.
3.△ABC中,AB=1,AC、BC是关于x的一元二次方程(m+5)x2-(2m-5)x+12=0两个根,外接圆O的面积为 ,求m的值.
,求m的值.
2.如图,通过防治“非典”,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图24-49所示,A、B、C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.
1.如图,⊙O是△ABC的外接圆,D是AB上一点,连结BD,并延长至E,连结AD,若AB=AC,∠ADE=65°,试求∠BOC的度数.

3.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.
2.边长为a的等边三角形外接圆半径为_______,圆心到边的距离为________.
1.经过一点P可以作_______个圆;经过两点P、Q可以作________个圆,圆心在_________上;经过不在同一直线上的三个点可以作________个圆,圆心是________的交点.
3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( )
A.
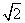 B.
B. C.
C.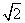 D.3
D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com