6、试一试：已知一个三角形的三个内角分别为、、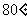，你能画出这个三角形吗？把你画的三角形与同伴画的进行比较，你发现了什么？

(所画出的三角形都是相似的，但大小不一定相同)。

三个对应角相等的两个三角形不一定全等。

5、练习：

　 P84 练习1、2

4、范例：

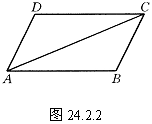　例1　如图24.2.2，四边形ABCD中，AD＝BC，AB＝DC，试说明△ABC≌△CDA.

　解：已知　　 AD＝BC，AB＝DC，

　　 又因为AC是公共边，由(S.S.S.)全等识别法，可知

　 　 △ABC≌△CDA

3、问题3、你用这个“SSS”三角形全等的识别法解释三角形具有稳定性吗？

(只要三角形三边的长度确定了，这个三角形的形状和大小就完全确定了)

2、问题2：你能用相似三角形的识别法解释这个(SSS)三角形全等的识别法吗？

(我们已经知道，三条边对应成比例的两个三角形相似，而相似比为1时，三条边就分别对应相等了，这两个三角形不但形状相同，而且大小都一样，即为全等三角形。)

1、问题1：如果两个三角形的三条边分别相等，那么这两个三角形会全等吗？

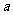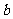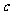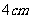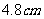做一做：给你三条线段、、，分别为、、，你能画出这个三角形吗？

先请几位同学说说画图思路后，教师指导，同学们动手画，教师演示并叙述书写出步骤。

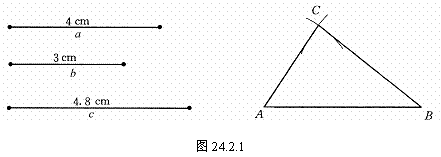
步骤：

(1)画一线段AB使它的长度等于c(4.8cm).

(2)以点A为圆心，以线段b(3cm)的长为半径画圆弧；以点B为圆心，以线段a(4cm)的长为半径画圆弧；两弧交于点C.

(3)连结AC、BC.

△ABC即为所求

把你画的三角形与其他同学的图形叠合在一起，你们会发现什么？

换三条线段，再试试看，是否有同样的结论

请你结合画图、对比，说说你发现了什么？

同学们各抒己见，教师总结：给定三条线段，如果它们能组成三角形，那么所画的三角形都是全等的。

这样我们就得到识别三角形全等的一种简便的方法： 如果两个三角形的三条边分别对应相等，那么这两个三角形全等．简写为“边边边”，或简记为(S.S.S.)。

请问同学，老师在黑板上画得两个三角形，△ABC与△全等吗？你是如何识别的。

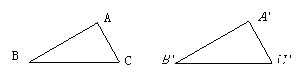
(同学们各抒己见，如：动手用纸摹下一个三角形，剪下叠到另一个三角形上，是否完全重合；测量两个三角形的所有边与角，观察是否有三条边对应相等，三个角对应相等。)

上一节课我们已经探讨了两个三角形只满足一个或两个边、角对应相等条件时，两个三角形不一定全

等。满足三个条件时，两个三角形是否全等呢？现在，我们就一起来探讨研究。

1．教材P.154中B组2．

3．常用的辅助线：

(1)两圆在各种情况下常考虑添连心线；

(2)两圆外切时，常添内公切线；

(3)两圆内切时，常添外公切线；

(4)计算公切线长时，常平移公切线，使它过其中一个圆的圆心．

2．公切线长的计算，都转化为解直角三角形，故解题思路主要是构造直角三角形．