
2、如果他只带了一个卷尺,能完成这个任务吗?
[问题1,学生可以回答去量斜边和一锐角,或直角边和一个锐角;但对于问题2,学生则难肯定]。
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?
问题:舞台背景的形状是两个直角三角形。工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆计划遮住无法测量。
1、你能帮他想个办法吗?
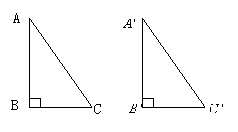 如图,△ABC和△
如图,△ABC和△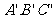 都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△
都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△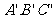 全等。并说明理由。
全等。并说明理由。
[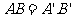 ,
,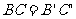 ,(SAS);
,(SAS);
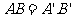 ,
,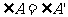 (ASA);
(ASA);
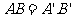 ,
,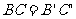 ,
,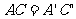 ,(SSS)
,(SSS)
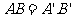 ,
,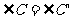 (AAS)]
(AAS)]
等,让学生抢答。
㈠创设情境
 ⒈“有两边及其中一边的对角对应相等,这两个三角形全等”对吗?
⒈“有两边及其中一边的对角对应相等,这两个三角形全等”对吗?
⒉你能画出符合上面的条件且全等的两个三角形吗?
㈡自主学习
⒈下面说法不正确的是 ( )
A.有一角和一边对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两角对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个直角三角形全等.
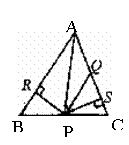
⒉如图,已知△ABC中,AQ=PQ, PR=PS,PR⊥AB于R,PS⊥AC于S,则 三个结论①AS=AR;②QP//AQ; ③△BRP≌△QSP中 ( )
A.全部正确 B-仅①和②正确 C.仅①正确 D.仅①和③正确
⒊下列命题:①两边及第三边上的高对应相等的两个三角形全 等;②两个三角形有一边及该边上的高及中线对应相等,那 么这两个三角形全等;③两边及第三边上的高对应相等的两 个锐角三角形全等;④有锐角为30'的两直角三角形,有一边
对应相等,则这两个三角形全等.其中正确的是
A.①② B.①③ C.③④ D.②③
㈢点拨矫正
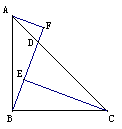
⒈如图AD为∠BAC的平分线,DF⊥AC于F,∠B=90°,DE=DC,试说明:BE=CF.

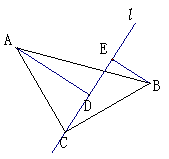
 ⒉如图已知∠ABC=90°,AB=BC,D为AC上一点,分别过点C、A作BD的垂线,垂足分别为E、F,试说明EF=CE-AF。
⒉如图已知∠ABC=90°,AB=BC,D为AC上一点,分别过点C、A作BD的垂线,垂足分别为E、F,试说明EF=CE-AF。
㈣规律总结
⒈利用证明两个三角形全等来证明两条线段相等是重要方法,而有时图形当中没有我们所要的三角形,就要添加辅助线构造三角形来帮助解题.
⒉证明两个直角三角形全等时,一定要分清用判定公理“HL",还是用一般的三角形全等的判定SAS;ASA,AAS,如果用“HL',,必须强调在直角三角形中”,如果用一般的判定,必须把直角对应相等转化为一个条件.
㈤尝试练习
 ⒈如图△ABC中,以AB为直径的⊙O,分别交AC、BC于D、E两点.若CD=CE,你能说明AD=BE吗?
⒈如图△ABC中,以AB为直径的⊙O,分别交AC、BC于D、E两点.若CD=CE,你能说明AD=BE吗?
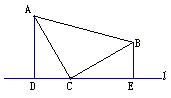
⒉已知:如图等腰直角三角形ABC中,∠ACB=90°,直线l过点C,AD⊥l,BE⊥l,垂足分别为D、E。
 (1)试说明图(1)中△ACD≌△CBE;
(1)试说明图(1)中△ACD≌△CBE;
(2)在图(2)中猜想△ACD与△CBE还全等吗?
⒈重点:HL公理的应用。
⒉难点:HL公理的推导。
⒈会利用HL的判定方法判定直角三角形全等。
⒉进一步熟练使用“分析综合法”探求解题思路。
P90习题24.2 1
本节课探讨出可用(SSS)来识别两个三角形全等,并能灵活运用(SSS)来识别三角形全等。三个角对应相等的两个三角不一定会全等。
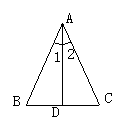
2、如图,AD是△ABC的中线,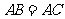 。
。 与
与 相等吗?请说明理由。
相等吗?请说明理由。
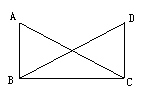
1、如图,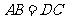 ,
,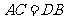 ,△ABC≌△DCB全等吗?为什么?
,△ABC≌△DCB全等吗?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com