通过本节课的学习，我们要学会灵活运用四种全等识别法，选择适当的方法来说明三角形的全等．同时，在证明过程中，还要注意运用两次全等及添加辅助线的方法来帮助解题．

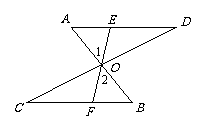例1 已知，如图，AB、CD互相平分于点O，过点O引直线EF分别与AD、BC相交于E、F两点．试说明AE＝BF．

解 因为AB、CD互相平分于点O，

所以AO＝BO，DO＝CO，

又因为∠AOD＝∠BOC(对顶角相等)，

所以由(S.A.S.)全等识别法，可知

△AOD≌△BOC．

所以∠A＝∠B(全等三角形的对应角相等)．

在△AOE和△BOF中，∠A＝∠B，AO＝BO，∠1＝∠2(对顶角相等)，

所以由(A.S.A.)全等识别法，可知

△AOE≌△BOF．

所以AE＝BF(全等三角形的对应边相等)．

例2 已知，CA＝CB，AD＝BD，M、N分别是CA、CB的中点，试说明DM＝DN．

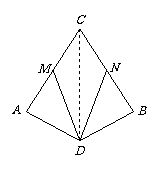分析 要证明DM＝DN，需先证明△ADM≌△BDN．而由已知条件，我们发现还缺少对应角相等，所以需要构造全等三角形．

解 连结CD，

因为CA＝CB，AD＝BD，CD是公共边，

所以由(S.S.S.)全等识别法，可知

△ACD≌△BCD．

所以∠A＝∠B(全等三角形的对应角相等)．

因为M、N分别是CA、CB的中点，且CA＝CB，

所以AM＝BN．

在△ADM和△BDN中，AM＝BN，∠A＝∠B，AD＝BD，

所以由(S.A.S.)全等识别法，可得

△ADM≌△BDN．

所以DM＝DN(全等三角形的对应边相等)．

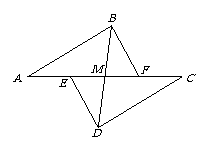问题1 已知，E、F分别为线段AC上的两个动点，且BF∥DE，若∠A＝∠C，AF＝CE，BD交AC于M点．试说明ME＝MF.

分析 要证明ME＝MF，需先证明△MED≌△MFB．在这对三角形中，可直接应用的相等条件只有一对对顶角相等，而由已知条件BF∥DE，又可得到一对角相等，但还缺一对等边．分析已知条件，易证△ABF≌△CDE，根据全等三角形对应边相等，可知BF＝DE．至此△MED≌△MFB所需条件已具备，问题得到解决．

解 因为BF∥DE，

所以∠BFA＝∠DEC(两直线平行，内错角相等)，

又因为AF＝CE，∠A＝∠C，

所以由(A.S.A.)全等识别法，可知

△ABF≌△CDE．

所以BF＝DE(全等三角形对应边相等)．

在△MED和△MFB中，

∠EMD＝∠FMB(对顶角相等)，∠DEM＝∠BFM， DE＝BF，

所以由(A.A.S.)全等识别法，可知

△MED≌△MFB．

所以ME＝MF(全等三角形对应边相等)．

　通过上例，我们可以知道，要证明两个三角形全等，有时不一定能从已知条件中直接得到结论，而需要借助于另一对三角形的全等．在解题时要仔细分析，灵活运用我们所知道的全等识别法，选取适当的方法来解决问题．

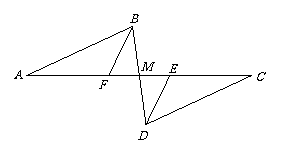
　问题2 在问题1中，如果我们把图形作如下改变，其余条件不变，请问结论还成立吗？

　你能说出识别三角形全等的方法有几种？具体内容是什么？

P90 习题24.2 　6

[教学反思]

学生谈谈收获、疑惑。总结本节学习直角三角形全等的识别，除了一般三角形全等识别法外，还有“HL”。

P89 练习1、2

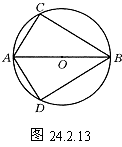
　 　如图24.2.13，AB是圆O的直径，AC＝AD，试说明△ABC和△ABD全等.

　解 　因为AB为⊙O的直径，所以

∠ACB＝∠ADB＝90°．

又　　 AC＝AD，AB＝AB，

由(H.L.)全等识别法，可知

△ABC≌△ABD

你可以用几种方法说明两个直角三角形全等？

试以两条线段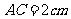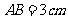，，分别为直角边和斜边在卡纸上画一个三角形。

按照下面的步骤做一做：

(1)作；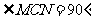

(2)在射线CM上截取线段；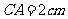

(3)以A为圆心，以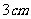长为半径画弧，交射线CN于点B；

(4)连结AB。

问：

(1)△ABC就是所求作的三角形吗？(是的)

　(2)剪下这个三角形，和其他同学所作的三角形进行比较，它们能重合吗？你发现了什么？

　 (能重合；发现：两个直角三角形的斜边及一条直角边分别对应相等，那么这两个直角三角形全等)

(3)你能用所学的知识来解决你的发现吗？

(由勾股定理可知，另一条直角边也是对应相等的)

因此可以得到如下结论：

如果两个直角三角形的斜边及一条直角边分别对应相等，那么这两个直角三角形全等. 简记为(H.L.)