
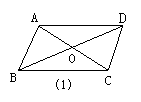
4.如图1所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
3.在△ABC和△A′B′C′,如果满足条件( ),可得△ABC≌△A′B′C′.
A.AB=A′B′,AC=A′C′,∠B=∠B′; B.AB=A′B′,BC=B′C′,∠A=∠A′
C.AC=A′C′,BC=B′C′,∠C=∠C′; D.AC=A′C′,BC=B′C′,∠B=∠B′
2.下列说法中,错误的是( )
A.全等三角形的面积相等; B.全等三角形的周长相等
C.面积相等的三角形全等; D.面积不等的三角形不全等
1.下列说法中正确的个数为( )
(1)所有的等边三角形都全等; (2)两个三角形全等,它们的最大边是对应边
(3)两个三角形全等,它们的对应角相等; (4)对应角相等的三角形是全等三角形
A.1 B.2 C.3 D.4
26.解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点 运动的时间为
运动的时间为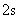 时,直线
时,直线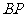 与⊙O相切.
与⊙O相切.
理由如下:
当点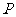 运动的时间为
运动的时间为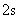 时,点
时,点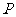 运动的路程为
运动的路程为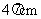 .
.
连接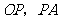 .∵⊙O的周长为
.∵⊙O的周长为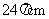 ,
,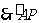 的长为⊙O周长的
的长为⊙O周长的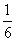 ,
,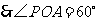 .
. 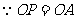 ,
,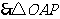 是等边三角形.
是等边三角形.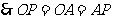 ,
,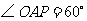 ,
,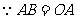 ,
,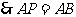 .
.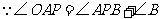 ,
,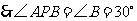 .
.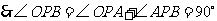 .
.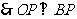 .
.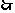 直线
直线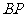 与⊙O相切.
与⊙O相切.
作者:马新华 山东省东营市利津县虎滩中学 257449答案:解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点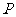 运动的时间为
运动的时间为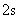 时,直线
时,直线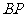 与⊙O相切.
与⊙O相切.
理由如下:
当点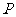 运动的时间为
运动的时间为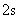 时,点
时,点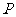 运动的路程为
运动的路程为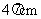 .
.
连接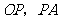 .∵⊙O的周长为
.∵⊙O的周长为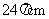 ,
,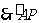 的长为⊙O周长的
的长为⊙O周长的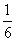 ,
,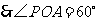 .
. 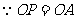 ,
,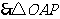 是等边三角形.
是等边三角形.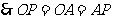 ,
,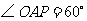 ,
,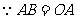 ,
,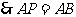 .
.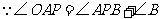 ,
,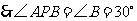 .
.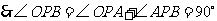 .
.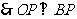 .
.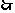 直线
直线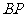 与⊙O相切.
与⊙O相切.
25.(1)过点P作直线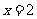 的垂线,垂足为A.
的垂线,垂足为A.
当点P在直线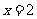 的右侧时,
的右侧时,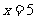 ,P(5,
,P(5,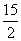 ).
).
当点P在直线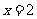 的左侧时,
的左侧时,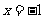 ,P(
,P(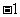 ,
,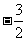 ).
).
∴当⊙P与直线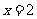 相切时,点P的坐标为(5,
相切时,点P的坐标为(5,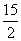 )或(
)或(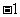 ,
,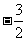 ).
).
(2)当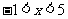 时,⊙P与直线
时,⊙P与直线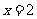 相交.
相交.
当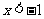 或
或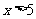 时,⊙P与直线
时,⊙P与直线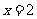 相离.
相离.
24.解:(1)依题意可知“合”“冲”“东方照”“西方照”时分别 如下图(1)、(2)、(3)、(4)所示:
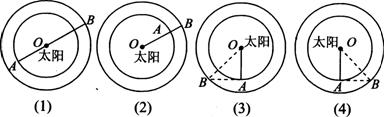
设O,A,B三点分别代表太阳,地球,火星.
“合”时,地球与火星之间的距离为AB=35.5(千万千米).
“冲”时,地球与火星之间的距离为AB=5.5(千万千米).
“东方照"时,地球与火星之间的距离为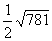 (千万千米).
(千万千米).
同理可求“西方照”时,地球与火星之间的距离为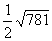 (千万千米).
(千万千米).
(2)从地球上发射宇宙飞船到火星,应选择在“冲”位置时,发射较好.
因为由(1)中的计算可知,此时地球离火星最近.
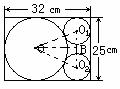
23.连结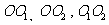 由题意得大圆的半径为9cm,设小圆的半径为r,在
由题意得大圆的半径为9cm,设小圆的半径为r,在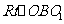 中可得
中可得 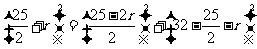 ,解得
,解得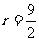 cm
cm
22.(1)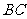 与⊙O相切.
与⊙O相切.
理由:连结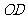 ,
,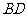 ,
,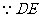 切⊙O于
切⊙O于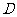 ,
, 为直径,
为直径,
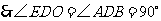 ,
,
又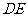 平分
平分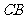 ,
,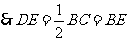 ,
,
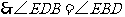 .又
.又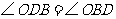 ,
, ;
;
 ,即
,即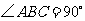 .
.
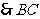 与⊙O相切.
与⊙O相切.
(2)当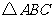 为等腰直角三角形
为等腰直角三角形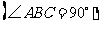 时,四边形
时,四边形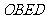 是平行四边形.
是平行四边形.
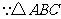 是等腰直角三角形
是等腰直角三角形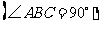 ,
,
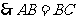 .
.
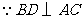 于
于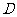 ,
,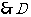 为
为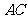 中点.
中点.
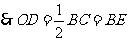 ,
,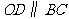 .
.
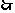 四边形
四边形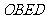 是平行四边形.
是平行四边形.
21.解:如图,∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com