6.带③去.

解:③中已知两角及其夹边作三角形是成立的,即已知:∠A、∠B及AB,求作的△ABC是惟一的,因此,应带③去.

5.解:∵在△ABC中,BD垂直平分AC,∴AD=DC,

又∵在△ADB和△CDB中,AD= CD,∠ADB=∠CDB,BD=BD,

∴△ADB≌△CDB,∴BA=BC.

　　 ∵CD=2cm,∴AD=2cm,∵∠DBC=45°,∴∠C=45°,

　　 ∴BD=2cm,在Rt△BCD中,有BD²+DC²=BC²,

∴BC=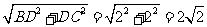, ∴AB=,

∵,∴

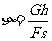4.证明:(1)作DF⊥AC,垂足为F,则∠DFA=90°,

∵∠B=90°, ∴∠B=∠DFA=90°.

在△ABD和△AFD中,∠1=∠2,∠B=∠DFA,AD=AD,

∴△ABD≌△AFD, ∴DB=DF,

又∵DF⊥AC,∴AC为⊙D的切线.

　　 (2)∵∠B=∠DFC=90°,

∴在Rt△BED和Rt△FCD中,DE=DC,DB=DF,

∴Rt△BED ≌Rt△FCD,∴BE=FC,

∵△ABD≌△AFD,∴AB=AF,

∵AC=AF+FC,∴AC=AB+BE.

3.证明:(1)∵∠ACB=90°,∴∠1+∠3=90°,

∵CF⊥AE,∴∠2+∠3=90°,∴∠1=∠2,

∵BD⊥BC,∴∠DBC=90°,∠DBC=∠ECA=90°,

在△ACE和△CBD 中,∠1=∠2,AC=CB,

∴∠ECA=∠DBC,∴△ACE≌△CBD,∴AE=CD.

(2)∵△CAE≌△BCD,∴CE=BD,

∵CE=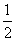BC,BC=AC,∴BD=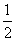AC,

∵AC=12,∴BD=6(cm)

2.CM=DE+DF,

证明:作DN⊥MC,垂足为N,

∵CM⊥AB,DE⊥AB,∴四边形EDNM是矩形,∴DE=MN,

∵BA⊥MC,DN⊥MC,∴DN∥BA,∴∠NDC=∠ABC,

∵AB= AC, ∴∠ABC=∠ACB,∴∠NDC=∠FCD,

∵DN⊥MC,DF⊥AC,∴∠DNC=∠CFD=90°.

在△DNC 和△CFD中,∠DNC=∠CFD,∠NDC=∠FCD,CD=DC,

∴△DNC≌△CFD,∴CN=DF,

∵CM=MN+NC, ∴CM=DE+DF.

1.解:∵△ADE是由△ADC折叠而得到的,∴△ADE≌△ADC,

∴∠DEA=∠DCA=90°,DE=DC,AE=AC,

设CD=xcm,则DE=x,DB=BC-CD=8-x,

∵AC=6,BC=8, ∴AB=,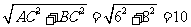

∴BE=AB-AE=AB-AC=10-6=4(cm),

在Rt△DBE中,由勾股定理得BD²=BE²+DE²,

∴(8-x)²=4²+x²,解得x=3(cm),即CD=3cm.

22.(2003,长沙)如图所示,若AC、BD、EF两两互相平分于点O, 请写出图中的一对全等三角形(只需写一对即可)_________.

B卷答案

21.(2003,福州)如图所示,已知点A、B、C、D在同一条直线上,AB=CD,∠D= ∠ECA,EC=FD,求证:AE=BF.

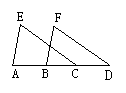
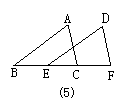
20.(2003,呼和浩特)如图5所示,在△ABC与△DEF中,如果AB=DE,BC=EF,只要再找出∠________=∠________或_________=_________,就可证明这两个三角形全等.

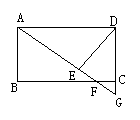
19.(2003,青岛)如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.

根据上述条件,请在图中找出一对全等三角形,并证明你的结论.