18.BD=CE.(只要能满足△ABD与△ACE全等的条件即可).

17.证明:如答图所示,

　　 ∵AD∥BC,∴∠A=∠C,

∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.

在△ADF和△CBE中, AD=CB,∠A=∠C,AF=CE,

∴△ADF≌△CBE,∴DF=BE.

14.20°　 15.D　 16.AH=CB(只要符合要求即求)

(三)

13.(1)证明:∵△ACM、△BCN是等边三角形,

∴∠1=∠2=60°,BC=CN,AC=CM,

∴∠1+∠3=∠2+∠3,即∠ACN=∠BCM,

在△ACN和△MCB中,AC=MC, ∠ACN=∠MCB,CN=CB,

∴△ACN≌△MCB,∴AN=MB.

　　 (2)AN=BM.理由如下,

∵四边形ACMF、BCNE为正方形,∴AC=MC,CN= CB,∠2=∠1.

在△ACN和△MCB中,AC=MC,∠2=∠1,CN=CB,

∴△ACN≌△MCB,∴AN=BM.

(二)

12.证法一:连结AC,由AB∥CD,有∠BAC=∠DCA,

又AB=CD,AC= CA得△ABC≌△CDA,

∴BC=DA,∴四边形ABCD是平行四边形.

　　 证法二:由法一知△ABC≌CDA,∴∠ACB=∠CAD,

　　 ∴BC∥AD,∴四边形ABCD是平行四边形.

　　 证法三:由法一知△ABC≌△CDA,∴∠B=∠D.

　　 又∵∠BAC=∠DCA,∠BCA=∠DAC,

∴∠BAC+∠DAC=∠DCA+∠BCA,即∠BAD= ∠BCD,

∴四边形ABCD是平行四边形.

　　 证法四:连结AC、BD,相交于点O,

∵AB∥CD,∴∠BAC=∠DCA,

∴∠ABO=∠CDO,又∵AB=CD,∴△ABO≌△CDO,∴AO=CO,BO=DO,

∴四边形ABCD是平行四边形.

　　 证法五:分别由A、D作BC的垂线,E、F为垂足,

∵AB∥CD,∴∠ABE= ∠DCF,

又∵AB=CD,∴Rt△ABE≌Rt△DCF,

∴AE=DF,∴四边形AEFD为矩形,

∴AD=EF= EF+BE-CF=BC,即AD=BC,

∴四边形ABCD是平行四边形.

11.解:原题答案:△AED≌△AFD;△AED≌△AFD,△BED ≌△CFD,△ABD≌△ACD.

　　 (1)答案:△ABD≌ACD,△ADE≌△ADF,△BDE≌△CDF,△AEM≌△AFM,△DEM ≌△DFM.

　　 (2)答案:△ABD≌△ACD,△ADE≌△ADF≌△BDE≌△CDF,△AEM≌△AFM ≌△DEM≌DFM.

10.已知:OM=ON,PM=PN.

　　 求证:OP平分∠AOB.

　　 证明:在△OPM和△OPN中,OM=ON,PM=PN,OP=OP,

∴△OPM≌△OPN,

∴∠POM=∠PON,故OP平分∠AOB.

9.已知:AB⊥BF,ED⊥BF,垂足分别为B,D,AE交BF于C,BC=DC.

　　 求证:DE=AB.

　　 证明:∵AB⊥BF,ED⊥BF,∴∠ABC=∠EDC=90°.

又∵∠BCA=∠DCE,BC=DE,

∴△BCA≌△DCE,∴AB=DE.

8.解:∵AC⊥AB,ED⊥DF,∴∠CAB=∠FDE=90°.

在Rt△ABC和Rt △DEF中,BC=EF,AC=DF,

∴Rt△ABC≌Rt△DEF,∴∠BCA=∠EFD,

∵AC⊥AB,∴∠ABC+ ∠BCA=90°,∴∠ABC+∠DFE=90°.

7.解:作A点关于直线CD的对称点A′,连结A′B,交CD于P,

则P 点为饮水处,线段AP+PB即为最短路程,

理由:

在△PAC和△PA′C中,CA=CA′,∠ACP=∠A′CP,PC=PC,

∴△PAC≌PA′C,∴AP=A′P,AC=A′C,

∵∠A′CP=∠BDP=90°,∠A′PC= ∠BPD,

∴△A′PC∽△BPD,∴,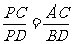

∵CD=PC+PD=800(米),A′C=AC=400,BD=300,

　 ∴,

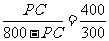　 ∴PC≈457(米),∴PD=CD-PC=800-457=343(米).

在Rt△APC中,PA=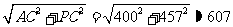 ( 米),

在Rt△BDP中,PB=,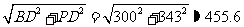

∴PA+PB=607+455.6≈1063(米).