1.(Ⅱ)(1)可行,由(SAS)全等识别法,证△ACB≌△DCE.

　　 (2)可行;由(ASA)全等识别法,证△ABC≌△EDC.

　　 (3)得∠ABC=∠EDC;成立.

　　 (4)能; ;AB=m·n

5.如图所示,一牧人带马群从A点出发,到草地MN放牧,在傍晚回到帐蓬B之前,先带马群到小河PQ去给马饮水.试问:牧人应走哪条路线才能使整个放牧的路程最短?

C卷答案

4.如图所示,已知△ABC,DG⊥BC,且G为BC的中点,∠A的平分线与DG交于D,DE⊥AB于E,DF⊥AC,交AC的延长线于F.

求证:BE=CF.

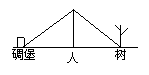
3.一次战役中,我军阵地与敌军碉堡隔河相望(如图所示),需要知道碉堡与我军阵地的距离,在不能过河测量又没任何测量工作的情况下,一个战士想出来这样一个办法;他面向碉堡的位置站好,然后调整帽子, 使视线通过帽檐正好落在碉堡的底部,然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上, 接着他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离,你能解释其中的道理吗?

2.如图3所示,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8cm,BC=10cm,求FC的长.

22.△DOF≌△BOE.

21.证明:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD.

在△EAC和△FBD中,AC=BD,∠ECA= ∠D,EC=FD,

∴△EAC≌△FBD,∴AE=BF.

20.∠B=∠DEF或AC=DF

19.△ABF≌△DEA.

　　 证明:∵矩形ABCD,

∴AB=CD,∴∠B=90°,AD∥BC,

∴∠AFB=∠DAE,

又∵DE=CD,∴AB=DE,

∵DE⊥AF,∴∠DAE=90°,

∴∠B=∠DEA.

在△AFB和△DAE中,∠AFB= ∠DAE,∠B=∠DEA,AB=DE,

∴△AFB≌△DAE.