
5.如果把三条边都n等分呢?
|
|
点 |
线段 |
全等三角形 |
|
n等分边 |
1+2+3+…+n+(n+1)=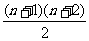 |
(1+2+3+…+n) ×3=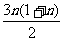 |
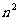 |
4.继续把三条边都分成五、六……等分,如图1、图2那样将分点连起来,数一数这时的点、线段和全等三角形的个数,看看与你的猜想是否符合;
由前面所得出的结论可推测出下列结论:
|
|
点 |
线段 |
全等三角形 |
|
五等分边 |
21=1+2+3+4+5+6 |
55=(1+2+3+4+5)×3 |
25=52 |
|
六等分边 |
28=1+2+3+4+5+6+7 |
73=(1+2+3+4+5+6)×3 |
36=62 |
|
…… |
…… |
…… |
…… |
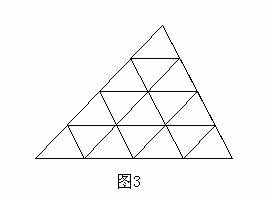
观察下图,验证我们发现的规律是正确的.
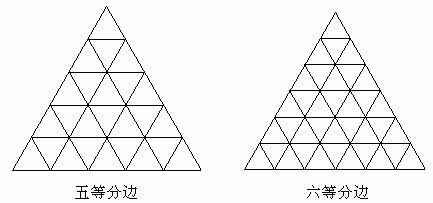
3.仔细分析所得到的一些数据,相互交流讨论,想一想其中有什么关系;
每增加一次等分,点的个数就增加(现在的等分数+1)个;线段的个数就增加(现在的等分数×3)个,而全等三角形的个数就是现在等分数的平方.
2.再把三条边都分成四等分,如图1、图2那样将分点连起来,数一数这时的点、线段和全等三角形的个数,也记录在相应的表格中;
 |
点 |
线段 |
全等三角形 |
|
四等分边 |
15 |
30 |
16 |
现在请你和你的同学一起参与如下的探索活动:演示
1.数一数图1、图2中的点、线段和全等三角形的个数,用一张表记录下来;
|
|
点 |
线段 |
全等三角形 |
|
二等分边 |
6 |
9 |
4 |
|
三等分边 |
10 |
18 |
9 |
回忆三角形全等的定义及判定的方法.
一个三角形两边中点的连线叫做这个三角形的中位线.
我们可以看到图1中三角形的三条中位线把这个三角形分成了4个小的三角形,而且这些小的三角形都是全等的.
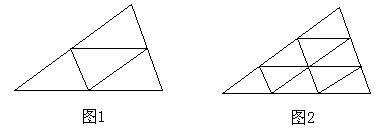
把三条边都分成三等分,再按图2将分点连起来,可以看到整个三角形被分成了9个小的三角形,而且这些小的三角形也都是全等的.
我们还可以把三条边都分成四等分,再如图1、图2那样将分点连起来,可以看到整修三角形被分成了一个个更小的全等三角形.
①作B点关于直线PQ的对称点B′;
②作B′点关于直线MN的对称点B″;
③连结AB″,交MN于C;
④连结CB′,交PQ于D;
⑤连结BD,则沿A→C→D→B的路线就是牧人应走的最短路线.
4.证明:连结DB、DC,∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF.∵GB=GC,DG⊥BC,∴DG是BC的垂直平分线,
∴DB=DC,∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°.
在Rt△DEB与Rt△DFC中,DB=DC,DE=DF,
∴Rt△DBE≌Rt△DCF,∴BE=CF.
3.解:∵AD⊥BC,∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,∠ADB= ∠ADC=90°,∠DAB=∠DAC,AD=AD,
∴△ADB≌△ADC,∴BD=CD.
2.解:设FC的长为xm,∵矩形ABCD,∴AD=BC=10(cm),∠B=∠D=90°.
∵△AEF是由△AED折叠而成,∴△AEF≌△AED,∴AF=AD=10,
在Rt△ABF中,∵BF=BC- FC=(10-x)cm,AB=8cm,AF=10cm,
∴AF2=AB2+BF2,∴102=82+(10-x)2,解得x=4或x= 16(舍去),
∴x=4,故FC=4(cm).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com