5．两个等圆⊙A和⊙B外切，过A点作⊙B的两条切线AC、AD，切点分别为

C、D，若AD＝2_，则BD＝_______．

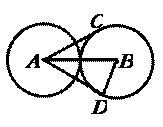
[考点扫描]考查两圆外切，圆心距与两圆半径之间的关系，以及切线的性质．

[分析点评]本题首先要明确两圆外切时圆心距与两圆半径之间的关系为

d＝R+r，由于两圆为等圆，则AB=2BD,再利用勾股定理构造方程求解.

[参考答案]2．

4．两圆半径之比为5∶3，外切时两圆圆心距是32cm，那么两个圆内切时圆心

距为_______cm.

[考点扫描]考查两圆相切时，圆心距与两圆半径之间的关系．

[分析点评]由题意，已知两圆的半径之比，因此本题可采用参数法，设两圆半径分别为5k、3k,则5k+3k=32 ， 　　

k=4，故两圆的半径分别为20和12．因此，两圆

内切时圆心距为两圆半径之差．

[参考答案]8．

3．已知⊙A和⊙B内切，⊙A半径为r₁=3cm，圆心距AB=1cm，则⊙B的半径r₂为________cm.

[考点扫描]本题主要考查了内切时，圆心距与两圆半径之间的关系以及

分类讨论思想．

[分析点评]本题要考虑两圆半径大小关系时，不仅要考虑⊙A的半径比⊙B的半径小的情况，还要考虑⊙A的半径比⊙B的半径大的情况．

[参考答案]2cm或4cm

2．已知⊙A和⊙B内切，它们的半径分别为3和1，过A作⊙B的切线，切点为C,则AC=______.

[考点扫描]考查两圆内切时，圆心距与两圆半径之间的关系与勾股定理的综合应用．

[分析点评]本题首先要明确AB＝3－1＝2，利用切线的性质和勾股定理求得

AC＝．

[参考答案]

解：因为C是切点，故连接BC、AB．在Rt△ABC中，AC=．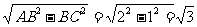

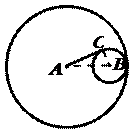
1．若半径为3cm和2cm的两圆相离，那么圆心距d(单位：cm)的取值范围是(　　　　 )

A．d＞5． 　B．d＜1．　 C．d＞5或d＜1．　 D．1＜d＜5．

[考点扫描]考查两圆相离，圆心距与两圆半径之间的关系.

[分析点评]本题要明确两圆相离有两种情况，即外离和内含，

故d＜R-r或d＞R+r.

[参考答案]C．

10．已知两圆的半径分别为R和r(R＞r),圆心距为d,关于x的方程有两个相等的实数根，则两圆的位置关系为______.

[考点扫描]考查圆和圆的位置关系与一元二次方程根的判别式的综合应用．

[分析点评]一元二次方程有两个相等的实数根，则△=0，R－d=±r,

即R+r=d或R－r=d．

[参考答案]相切(外切或内切)．

[能力提升]

9．三角形三边长分别为4cm、5cm、6cm，以各顶点为圆心的三个圆两两外切，则各圆的半径分别为______cm.

[考点扫描]考查两圆外切，圆心距与两圆半径之间的关系，以及方程思想的运用．

[分析点评]本题要明确两圆外切时，圆心距与两圆半径之间的关系是圆心距d=R+r，若设三个圆的半径分别是xcm、ycm、zcm，由题意得　解之得，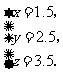

[参考答案]1.5cm 、2.5cm 、3.5cm．

8．已知半径分别为3 cm、4cm的⊙A和⊙B两圆外切，那么半径为6cm且与这两个圆都相切的圆有_____个．

[考点扫描]考查两圆相切时，圆心距与两圆半径之间的关系，以及分类讨论的数学思想．

[分析点评]两圆相切包括内切和外切，故解题时要分类讨论．如图，与⊙A、⊙B 均外切的有⊙E和⊙F，与⊙A内切且与⊙B 外切的有⊙D，与⊙A外切且与⊙B 内切的有⊙C，故共有4个．

[参考答案]4．

7．若⊙A的圆心坐标为(2，0)，半径为1，⊙B的圆心坐标为(－1，0)，半径为3，则这两圆的位置关系是_____．

[考点扫描]考查圆和圆的位置关系与直角坐标系的综合应用.　　　　　　

　 [分析点评]本题首先计算出圆心距AB，然后确定AB与两圆半径的和、差之间的大小关系,由已知AB=3，R+r=4，R－r＝2，可得出两圆相交．

　 [参考答案]相交．

6．两圆的直径分别为3+r和3－r，若它们的圆心距为r，则两圆的

位置关系为_____.

[考点扫描]考查圆和圆的位置关系的判定.

[分析点评]题目中给出的条件是两圆的直径，则两圆的半径分别

为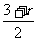、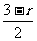_{，两圆半径之差为r，圆心距也为r，}

_{故两圆内切．}

[参考答案]内切．