3．施工工地的水平地面上有三根外径都是1的水泥管两两相切地堆放在一起，则其最高点到地面的距离为__________.

[考点扫描]考查两圆外切，圆心距与两圆半径之间的关系以及等

边三角形的性质的综合应用．

[分析点评]本题首先要明确三个圆的直径均为1，且两两外切，所以△ABC为等边三角形．本题的实质是求点D到直线的距离，即DF的长度．因此，两圆相切连心线必过切点以及勾股定理是解决本题的关键．

[参考答案]解：如图，设⊙C与⊙B切于点E，连接BC，则BC过点E，连接AB、AC、AE，延长AE交直线于F，延长EA交⊙A于点D．

在Rt△ABE中，AE＝，

∴DF＝1+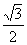．∴其最高点到地面的距离为1+．

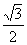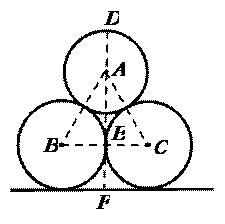
2．⊙E和半圆F内切于点C，与半圆的直径AB切于点D．若AB=6，⊙E的半径为1，则∠ABC=__________.

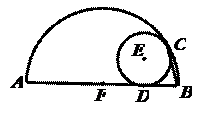
[考点扫描]考查两圆外切时圆心距与两圆半径之间的关系、两圆相切的性质等知识的综合应用．

[分析点评]本题首先要明确直线和圆相切时常用的辅助线是连接圆心与切点，构造直角三角形．同时要熟记两圆相切连心线必定经过切点这一重要性质． 连接FC、ED，则E 、F、C 三点共线．EF=3-1=2． 在Rt△EFD中，利用 EF=2DE,

求得∠EFD=30°,利用三角形的内角和定理计算∠ABC的度数．

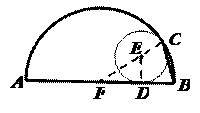
[参考答案]∠ABC=75°．

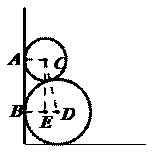
1．两圆轮叠靠在墙边，已知两轮半径分别为4和1，则它们与墙的切点A、B之间的距离为_________.

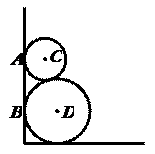
[考点扫描]考查两圆外切时圆心距与两圆半径之间的关系与切线性质的

综合应用．

[分析点评]本题首先要明确两圆外切时d＝R+r，连接CD、AC、BD，

得直角梯形ABDC，再将直角梯形转化为矩形和直角三角形．

过点C作CE⊥BD，垂足为E，则四边形ABEC是矩形．

在Rt△CDE中，CD＝4+1＝5，DE＝4-1＝3，

则CE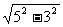＝＝4, 从而AB＝CE＝4.

[参考答案]4．

12．若⊙O₁和⊙O₂相交于A、B两点，⊙O₁和⊙O₂的半径分别为和2，

公共弦长为2，∠O₁AO₂的度数为 _________.

[考点扫描]本题主要考查了两圆相交，圆心距与两圆半径之间的关系以及分类讨论的思想．

[分析点评]本题要明确两圆相交,连心线垂直平分公共弦．同时本题要注意两圆相交，两圆圆心的位置可能在公共弦的同侧，也可能在异侧,更具体地体现了数学分类讨论思想．

①当两圆圆心的位置在公共弦的异侧时如图1：

连接AB、O₁O₂相交于点E，连接AO₁、AO₂．

根据题意得O₁O₂垂直平分AB，所以AE＝1．

在Rt△AEO₁中，O₁E=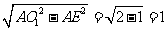∴∠O₁AE＝45°．

在Rt△AEO₂中，AE=1，AO₂＝2，∴∠AO₂E＝30°，

则∠O₂AE＝60°，∴∠O₁AO₂＝60°+45°＝105°

②当两圆圆心的位置在公共弦的同侧时如图2：

连接O₂O₁并延长交AB于点E，连接AO₁、AO₂．

同理可求∠O₁AE＝45°，∠O₂AE＝60°．

∴∠O₁AO₂＝60°－45°＝15°．

∴∠O₁AO₂的度数为105°或15°．

[参考答案]105°或15°．

[拓展延伸]

11．⊙A和⊙B外切，又同时与⊙O内切，若△OAB的周长为20cm,则⊙O的

半径为__________.

[考点扫描]考查两圆外切、内切时，圆心距与两圆半径之间

的关系以及方程思想的综合应用．

[分析点评]本题首先要明确两圆外切时圆心距与两圆半径之间的关系为

d＝R+r，内切时d＝R－r.设⊙A、⊙B、⊙O的半径分别为

x、y、z，则由题意得，z－x+z－y+x+y=20,2z=20，z=10.

[参考答案]10cm．

10．已知⊙O₁和⊙O₂的半径都等于1，则下列命题参考的有_________.

(1)若O₁O₂＝1，则⊙O₁和⊙O₂有两个公共点.

(2)若O₁O₂＝2，则两圆外切．

(3)若O₁O₂≤3，则⊙O₁和⊙O₂必有公共点.

(4)若O₁O₂＞1，则两圆不会相切．

[考点扫描]考查圆和圆的位置关系的判定.

[分析点评]本题要明确圆和圆的五种位置关系中圆心距与两圆半径之间的

关系．设两圆半径分别为R和r,圆心距为d, 由题意得，R+r=2　

R－r=0故(1)、(2)参考.而(3)中d≤3不能确定d与R+r

和R－r大小，例如当d=0时，两圆重合必有公共点，当d=3时两圆外离，无公共点.(4)中当d=2时两圆外切.

[参考答案](1)、(2).

9．⊙A和⊙B的半径分别为R和r，且R²+r²－4R－2r+5＝0，两圆的圆心距

d＝1，则⊙A和⊙B的位置关系为　________.

[考点扫描]考查圆和圆的位置关系与配方法的综合应用．

[分析点评]由方程R²+r²－4R－2r+5＝0得(R－2)²+(r－1)²=0，

则R＝2 ，r＝1，所以d＝R－r．

[参考答案]内切．

8．⊙A和⊙B的半径分别为R和r,圆心距AB=5 ，R=3．当0＜r＜2时，⊙A和⊙B的位置关系为________.

[考点扫描]本题主要考查了圆和圆的位置关系的判定．

[分析点评]本题首先要明确圆和圆的五种位置关系中圆心距与两圆半径

之间的关系，由题意AB=5 ，R=3，0＜r＜2,则AB>3+r可以

判断两圆外离．本题也可以采用特殊值代入法．

　 [参考答案]外离．

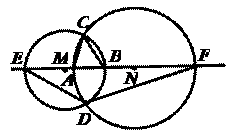
7．如图⊙M和⊙N相交于C、D两点，直线AB经过圆心交两圆于E、F两点．若∠ACB＝40°，则∠EDF＝_____.

[考点扫描]考查圆周角定理和化归的思想．

[分析点评]在两圆相交问题中，连接公共弦是常作的辅助线，在本题中连接CD，则∠EFD=∠ACD，∠FED=∠BCD．利用三角形的内角和定理求解．

[参考答案]140°.

6．⊙A和⊙B相交于C、D两点，⊙A的半径为10，⊙B半径为17，两圆的公

共弦长16，则两圆的圆心距为__________.

[考点扫描]考查两圆相交时，圆心距与两圆半径之间的关系以及分类讨论的思想．

[分析点评]本题首先要明确两圆相交,连心线垂直平分公共弦．同时本题要注意两圆相交，两圆圆心的位置可能在公共弦的同侧，也可能在异侧．

①当两圆圆心的位置在公共弦的异侧时如图1：

连接AB、CD 相交于点E，连接AC、BC．

根据题意得AB垂直平分CD，所以CE＝8．

在Rt△AEC中，AE＝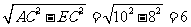

同理可求BE＝15，所以AB＝15+6＝21．

②当两圆圆心的位置在公共弦的同侧时如图2：

连接BA并延长交CD于点E，连接AC、BC．

同理可求BE＝15 ，AE＝6，所以AB＝15－6＝9．

以两圆圆心距为21或9．

[参考答案]21或9．