5、垂径定理及其推论：

定理及推论1：直线过圆心、垂直弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧这五要素中用其中两个要素做条件就能推导出其它三个要素都成立。若用过圆心、平分弦做条件时要强调被平分的弦不是直径。

推论2：平行弦所夹的弧相等。

4、过三点的圆(三角形的外心)

经过三角形三个顶点的圆叫三角形外接圆；外接圆的圆心叫三角形的外心；三角形的外心是三条边中垂线的交点，到三个顶点距离相等；直角三角形外心在斜边上、锐角三角心外心在三角形内、钝角三角形外心在三角形外。

3、弦、直径、孤、弓形、半圆、同心圆、等圆、等孤等概念

等弧一定要强调要在同圆或等圆中；半圆不包括直径。

2、点和圆的位置关系：

在圆内、在圆上、在圆外(由点和圆心的距离与圆的半径大小来确定)

1、圆的定义：

到定点的距离等于定长的点的集合

1.如图，是2004年5月5日2时48分到3时52分在北京拍摄的从初亏到食既的月全食过程.

(1)

(2)　　　　　　　　　 (3)　　　　　　　 (4)

用数学的眼光看图(1)，可以认为是地球、月球投影(两个圆)的位置关系发生了从相切、相交到内切的变化；2时48分月球投影开始进入地球投影的黑影(图(2))；接着月球投影沿着直线OP匀速地平行移动进入地球投影的黑影(图(3))；3时52分，这时月球投影全部进入地球投影的黑影(图(4)).设照片中的地球投影如图(2)中半径为R的大⊙O，月球投影如图(2)中半径为r的小⊙P，求这段时间内圆心距OP与时间t(分)的函数关系式，写出自变量的取值范围.

[考点扫描]本题考查的是圆和圆的位置关系的定义．

[分析点评]本题实质是从月全食过程中抽象出圆和圆的位置关系，从中归纳

出圆心距OP与时间t的函数关系．

[参考答案]

解：这段时间从2时48分到3时52分共64分钟，在这段时间内点P运动的路程为2r，如图(5)

(5)

∴点P运动的速度为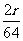，即，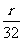

∴点P在t分钟内运动的速度为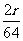t，

∴OP＝R+r-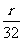t(0≤t≤64).

6．在两个同心圆中，大圆的弦AB交小圆于C、D两点，设大圆与小圆的半径分别为a、b．求证：AD·BD= a²－b²_．

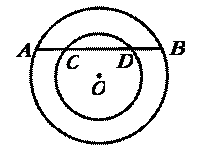
[考点扫描]考查两圆内含时、垂径定理、勾股定理的综合应用．

[分析点评]本题在证明过程中主要运用垂径定理和勾股定理，而因式分解

的应用起着重要的作用．在证明过程中，利用平方差把两条线段平方差转化为它们的和与差的乘积，使之更接近于常规图形，便于证明．

[参考答案]

证明：作OE⊥AB，垂足为E．连接OA、OC，则OA＝a，OC＝b．

　 　在直角三角形AOE中，AE²＝OA²－OE²，

在直角三角形COE中，CE²＝OC²－OE² ．

所以AE²－CE²＝a²－b²， 即(AE+CE)(AE－CE)＝a²－b²．

　　　 由垂径定理可得，AE＝BE，CE＝DE，

又AE+CE＝AD，AE－CE＝BD，

所以 AD·BD＝a²－b²．

[数学花苑]

[聪明屋]

5．两个同样大小的肥皂泡黏在一起，其剖面图如图所示(其中A、B是圆心)分隔成两个肥皂泡的肥皂膜PQ成一条直线，TP、NP分别为两圆的切线．

求∠TPN的大小．

[考点扫描]考查两等圆相交的性质与等边三角形的性质的

综合应用．

[分析点评]如果两个等圆相交，圆心距等于半径的长，则两个圆心与任何一个交点组成的三角形都是等边三角形．本题以实际背景抽象成一道数学问题，具有很强的趣味性．

[参考答案]解：连接AB、PA、PB．

∵PA=PB=AB ，

∴△PAB是等边三角形．

∴∠APB=60°，

∵TP与NP分别为两圆的切线，

　　　　　　　　 ∴∠TPA=∠NPB=90°．

　　　　　　　　 ∴∠TPN=360°－2×90°－60°＝120°．

4．今有一圆形硬币，在这硬币的周围排列几枚同样大小的硬币，使所有的硬币都与这枚硬币相切，并彼此外切，则需硬币多少枚？

[考点扫描]考查相切两圆的定义及性质．

[分析点评]本题的关键是在这硬币的周围排列几枚同样大小的硬币，这就意味着这些都是等圆，且相邻的硬币外切．因此，外周每两

个圆的圆心与这个圆的圆心构成等边三角形，其圆心角等于

60°，相当于把圆六等分．

[参考答案]需要硬币6枚．