20．如图11，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC²=PE·PO．(1)求证：PC是⊙O的切线；(2)若OE∶EA=1∶2， PA=6，求⊙O的半径；(3)求sinPCA的值．(12分)

19．如图10，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E，求证：

(1) AC是⊙O的切线．(2)若AD∶DB=3∶2，AC=15，求⊙O的直径．(12分)

图10

18．如图9，AB是⊙O的直径，点D在AB的延长线上，且BD=OB，点C在⊙O上，∠CAB=30°，求证：DC是⊙O的切线．(10分)

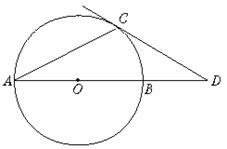
图9

17．如图8，已知AB是⊙O的直径，AC切圆O于A，CB交圆O于D，AC=2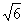，CD=3，求tanB的值．(10分)

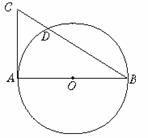
图8

16．如图7，在⊙O中，P是直径AB上一动点，在AB同侧作AA′⊥AB， BB′⊥AB，且AA′=AP，BB′=BP，连结A′B′，过点P从点A移到点B时，A′B′的中点的位置

A．在平分AB的某直线上移动

B．在垂直AB的某直线上移动

C．在弧AMB上移动

D．保持固定不移动

15．如图6，BC是⊙O直径，点A为CB延长线上一点，AP切⊙O于点P，若AP=12，AB∶BC=4∶5，则⊙O的半径等于

A．4　　　　　　　　 B．5　　　　　　　　 C．6　　　　　　　　 D．7

14．如图5，点P为弦AB上一点，连结OP，过PC作PC⊥OP，PC交⊙O于C，若AP=4， PB=2，则PC的长是

A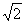．　　　　　　 B．2　　　　　　　　 C．2　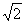　　　　　 D．3

13．如图4，AB是⊙O的直径，弦AC、BD相交于P，则CD∶AB等于

A．sinBPC　　　　　 B．cosBPC　　　　　 C．tanBPC　　　　　 D．cotBPC

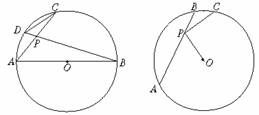
图4　　　　 图5　　　　 图6　　　　图7

12．在⊙O中，弦AB和CD相交于点P，若PA=4，PB=7，CD=12，则以PC 、PD 的长为根的一元二次方程为

A．x²+12x+28=0

B．x²－12x+28=0

C．x²－11x+12=0

D．x²+11x+12=0

11．P是⊙O外一点，PA、 PB切⊙O于点A、B，Q是优弧AB上的一点，设∠APB=α，∠AQB=β ，则α与β的关系是

A．α=β　　　　　　　　　　　　　　　　 B．α+β=90°

C．α+2β=180°　　　　　　　　　　　　 D．2α+β=180°