
4.运用以上的知识解决实际问题.
3.画正多边形的方法.
2.正多边形的半径、正多边形的中心角、边长、正多边的边心距之间的等量关系.
本节课应掌握:
1.正多边和圆的有关概念:正多边形的中心,正多边形的半径,正多边形的中心角,正多边的边心距.
例3.在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6.
(1)求△ABC的边AB上的高h.
(2)设DN=x,且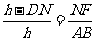 ,当x取何值时,水池DEFN的面积最大?
,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
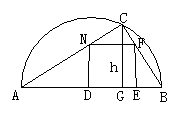
分析:要求矩形的面积最大,先要列出面积表达式,再考虑最值的求法,初中阶段,尤其现学的知识,应用配方法求最值.(3)的设计要有新意,应用圆的对称性就能圆满解决此题.
解:(1)由AB·CG=AC·BC得h=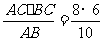 =4.8
=4.8
(2)∵h=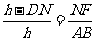 且DN=x ∴NF=
且DN=x ∴NF=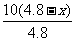
则S四边形DEFN=x·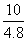 (4.8-x)=-
(4.8-x)=-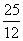 x2+10x
x2+10x
=-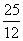 (x2-
(x2-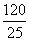 x)=-
x)=-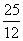 [(x-
[(x-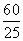 )2-
)2-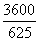 ]=-
]=-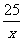 (x-2.4)2+12
(x-2.4)2+12
∵-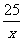 (x-2.4)2≤0 ∴-
(x-2.4)2≤0 ∴-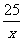 (x-2.4)2+12≤12 且当x=2.4时,取等号
(x-2.4)2+12≤12 且当x=2.4时,取等号
∴当x=2.4时,SDEFN最大.
(3)当SDEFN最大时,x=2.4,此时,F为BC中点,在Rt△FEB中,EF=2.4,BF=3.
∴BE=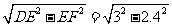 =1.8
=1.8
∵BM=1.85,∴BM>EB,即大树必位于欲修建的水池边上,应重新设计方案.
∵当x=2.4时,DE=5
∴AD=3.2,
由圆的对称性知满足条件的另一设计方案,如图所示:

此时,AC=6,BC=8,AD=1.8,BE=3.2,这样设计既满足条件,又避开大树.
教材P115 练习1、2、3 P116 探究题、练习.
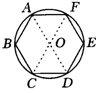 如果我们以正多边形对应顶点的交点作为圆心,过点到顶点的连线为半径,能够作一个圆,很明显,这个正多边形的各个顶点都在这个圆上,如图,正六边形ABCDEF,连结AD、CF交于一点,以O为圆心,OA为半径作圆,那么肯定B、C、D、E、F都在这个圆上.
如果我们以正多边形对应顶点的交点作为圆心,过点到顶点的连线为半径,能够作一个圆,很明显,这个正多边形的各个顶点都在这个圆上,如图,正六边形ABCDEF,连结AD、CF交于一点,以O为圆心,OA为半径作圆,那么肯定B、C、D、E、F都在这个圆上.
因此,正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
我们以圆内接正六边形为例证明.
如图所示的圆,把⊙O分成相等的6段弧,依次连接各分点得到六边ABCDEF,下面证明,它是正六边形.
 ∵AB=BC=CD=DE=EF
∵AB=BC=CD=DE=EF
∴AB=BC=CD=DE=EF
又∴∠A=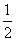 BCF=
BCF=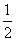 (BC+CD+DE+EF)=2BC
(BC+CD+DE+EF)=2BC
∠B=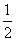 CDA=
CDA=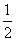 (CD+DE+EF+FA)=2CD
(CD+DE+EF+FA)=2CD
∴∠A=∠B
同理可证:∠B=∠C=∠D=∠E=∠F=∠A
又六边形ABCDEF的顶点都在⊙O上
∴根据正多边形的定义,各边相等、各角相等、六边形ABCDEF是⊙O的内接正六边形,⊙O是正六边形ABCDEF的外接圆.
为了今后学习和应用的方便,我们把一个正多边形的外接圆的圆心叫做这个多边形的中心.
外接圆的半径叫做正多边形的半径.
正多边形每一边所对的圆心角叫做正多边形的中心角.
中心到正多边形的一边的距离叫做正多边形的边心距.
 例1.已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正六边形的周长和面积.
例1.已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正六边形的周长和面积.
分析:要求正六边形的周长,只要求AB的长,已知条件是外接圆半径,因此自然而然,边长应与半径挂上钩,很自然应连接OA,过O点作OM⊥AB垂于M,在Rt△AOM中便可求得AM,又应用垂径定理可求得AB的长.正六边形的面积是由六块正三角形面积组成的.
解:如图所示,由于ABCDEF是正六边形,所以它的中心角等于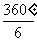 =60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,所求的正六边形的周长为6a
在Rt△OAM中,OA=a,AM=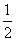 AB=
AB=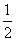 a 利用勾股定理,可得边心距
a 利用勾股定理,可得边心距
OM=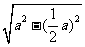 =
=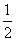
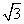 a
a
∴所求正六边形的面积=6×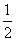 ×AB×OM=6×
×AB×OM=6×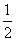 ×a×
×a× a=
a=
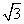 a2
a2
现在我们利用正多边形的概念和性质来画正多边形.
例2.利用你手中的工具画一个边长为3cm的正五边形.
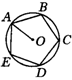 分析:要画正五边形,首先要画一个圆,然后对圆五等分,因此,应该先求边长为3的正五边形的半径.
分析:要画正五边形,首先要画一个圆,然后对圆五等分,因此,应该先求边长为3的正五边形的半径.
解:正五边形的中心角∠AOB=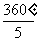 =72°,
=72°,
如图,∠AOC=30°,OA=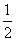 AB÷sin36°=1.5÷sin36°≈2.55(cm)
AB÷sin36°=1.5÷sin36°≈2.55(cm)
画法(1)以O为圆心,OA=2.55cm为半径画圆;
(2)在⊙O上顺次截取边长为3cm的AB、BC、CD、DE、EA.
(3)分别连结AB、BC、CD、DE、EA.
则正五边形ABCDE就是所要画的正五边形,如图所示.
2.实例略.正多边形是轴对称图形,对称轴有无数多条;正多边形是中心对称图形,其对称中心是正多边形对应顶点的连线交点.
2.从你身边举出两三个正多边形的实例,正多边形具有轴对称、中心对称吗?其对称轴有几条,对称中心是哪一点?
老师点评:1.各边相等,各角也相等的多边形是正多边形.
请同学们口答下面两个问题.
1.什么叫正多边形?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com