
证明的一般步骤:
1.审题:分清命题的“题设”和“结论”;
例1 证明:一条直线截两条平行直线所得的内错角相等.
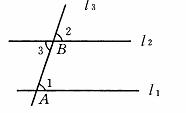
已知:如图,直线l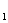 ∥l
∥l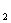 ,直线l
,直线l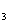 分别和l
分别和l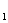 、 l
、 l 相交于点A、B.
相交于点A、B.
求证:∠1=∠3.
 证明:因为l
证明:因为l ∥l
∥l ,(已知)
,(已知)
所以∠1=∠2,(两直线平行,同位角相等)
又∠2=∠3,(对顶角相等)
所以∠1=∠3.(等量代换)
例2 证明:同角的余角相等.?
已知:如图,∠2是∠1的余角,∠3是∠1的余角.
求证:∠2=∠3.?
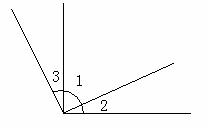 证明:因为∠2与∠1互为余角,(已知)
证明:因为∠2与∠1互为余角,(已知)
∠3与∠1互为余角,
所以∠2+∠1=90°,∠3+∠1=90°,?(余角定义)
所以∠2+∠1=∠3+∠1,?(等量代换)
则∠2=∠3.?(等量减等量差相等)
上面几个例子说明:通过特殊的事例得到的结论可能正确,也可能不正确.因此,通过这种方式得到的结论,还需进一步加以证实.
根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明(proof).
前面的学习已经告诉我们:一条直线截两条平行线所得的内错角相等.下面我们运用前面所提到的基本事实,即公理来证明这个结论.
一位同学在钻研数学题时发现:
2+1=3,
2×3+1=7,
2×3×5+1=31,
2×3×5×7+1=211.
于是,他根据上面的结果并利用素数表得出结论:从素数2开始,排在前面的任意多个素数的乘积加1一定也是素数.他的结论正确吗?
如图所示,

一个同学在画图时发现:三角形三条边的垂直平分线的交点都在三角形的内部.于是他得出结论:任何一个三角形三条边的垂直平分线的交点都在三角形的内部.他的结论正确吗?
我们曾经通过计算四边形、五边形、六边形、七边形、八边形的内角和,得到一个结论:n边形的内角和等于180°(n-2).这个结论可靠吗?是否有一个多边形的内角和不满足这一规律?
2.证明:矩形的两条对角线长相等.
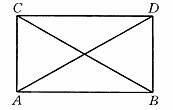
1.证明:平行四边形的两组对边分别相等.

4.证明命题的一般步骤是什么?(审题、译题、想题、证题)
3.假命题应怎样判定?
2.公理的正确性怎样判定?定理的正确性怎样判定?
1.命题、公理、定理之间的关系是什么?(关系图)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com