
5.如图所示,△ABC的周长为a,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2……,如此进行下去得△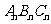 ,则:
,则:
(1)△A1B1C1的周长为________,(2)△A2B2C2 的周长为______ ,……,
(n) △ 的周长为_______.
的周长为_______.
C卷答案:
4.如图所示,ABCD是一块四边形菜地的示意图,EFG是流过这块菜地的水渠,水渠东边的地属张家承包,水渠西边的地属李家承包,现在村委会在田园规划中需要将流经菜地的水渠取道,并且要保持张、李两家的承包土地面积不变,请你设计一个挖渠的方案,就在给出的图形上面画出设计示意图,并说明理由.

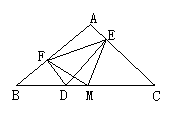
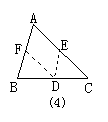
3.如图所示,已知在Rt△ABC,AB=AC,∠A=90°点D为BC上任一点,DF⊥AB于F, DE⊥AC于E,M为BC的中点,试判断△MEF是什么形状的三角形,并证明你的结论.
2.一个零件的形状如图所示,按规定∠A应等于90°,∠B和∠C应分别是30 °和21°,检验工人量得∠BDC=148°, 就断定这个零件不合格运用三角形的有关知识说明零件不合格的理由.
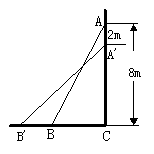
1.一个长为10m的梯子斜靠在墙上,如图所示, 梯子的顶端距地面的垂直距离为8m,梯子的顶端下滑2m后,底端将水平滑动2m吗?试说明理由.
(三)
13.解:方案(2):若这个角是两边的夹角,则这两个三角形全等.
方案(3):若这个角是直角,则这两个三角形全等.
方案(4):若这两个三角形是锐角三角形,则这两个三角形全等.
(二)
11.证法一:如答图1所示,过C作CD∥AB,∴∠B=∠BCD,∵AB∥EF,CD∥AB,
∴CD∥EF,∴∠F=∠DCF,∴∠BCD+∠DCF=∠B+∠F,即∠BCF=∠B+∠F.
证法二:如答图2所示,过C作DC∥AB,∴∠B+∠BCD=180°,
∵AB∥EF,DC ∥AB, ∴DC∥EF,∴∠DCF+∠F=180°,∴∠B+∠BCD+∠DCF+∠F=360°,
∴∠B+∠F=360°-(∠BCD+∠DCF)=∠BCF,即∠BCF=∠B+∠F.
证法三:如答图3所示,延长BC交EF于D,∵AB∥EF,∴∠CDF=∠B,
∵∠BCF=∠CDF+ ∠F,∴∠BCF=∠B+∠F.

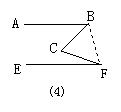
证法四:如答图4所示,连结BF,∵AB∥EF,
∴∠ABF+∠EFB=180°,
即∠ABC+∠CBF+∠BFC+∠CFE=180°,
∴∠ABC+∠CFE=180°-(∠CBF+∠BFC)= ∠BCF,
即∠BCF= ∠ABC+∠EFC.
证法五:如答图5所示,过B作CF的平行线,交EF的延长线于D,
∵AB∥EF,∴∠GBA= ∠D.∵BD∥CF,∴∠CFE=∠D,
∴∠GBA=∠CFE,BD∥CF,
∴∠BCF=∠CBG=∠ABC+∠GBA=∠ABC+∠CFE,即∠BCF=∠ABC+∠CFE.
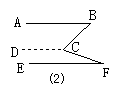
12.证法一:如图1所示,作BC的延长线CD,在△ABC的外部,以CA为一边,CE 为一边画∠1=∠A,∴CE∥BA,∴∠B=∠2.∵∠1+∠2+∠ACB=180°,∴∠A+∠B+∠ACB=180°
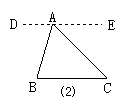

证法二:如答图2所示,过A作BC的平行线DE,∴∠B=∠DAB,∠C=∠EAC.
∵∠DAB+∠BAC+∠EAC=180°,∴∠BAC+∠B+∠C=180°.
证法三:如答图3所示,过B作CA的平行线DB,
则有∠DBA=∠A,∠DBA+ ∠ABC+ ∠C=180°.∴∠A+∠ABC+∠C=180°.
证法四:如答图4所示,在BC上取一点D,过D分别作AB、AC的平行线交AC、AB于E、F,则有四边形AFDE为平行四边形,所以∠FDE=∠A,∠EDC=∠B,∠FDB=∠C.
∵∠EDC+ ∠FDE+∠FDB=180°,∴∠A+∠B+∠C=180°.
10.原题答案:证明:在△AOP和△BOP中,OA=OB,OP=OP,PA=PB,
∴△AOP≌△BOP,∴∠1=∠2,即OP平分∠AOB.
变形题答案:证明:在△AOP和△BOP中,OA=OB,∠2=∠1,OP=OP,
∴△AOP ≌△BOP,∴PA=PB.
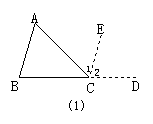
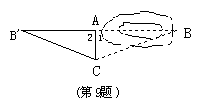
9.已知:如答图所示,在△BB′C中,CA⊥BB′,垂足为A,∠ACB′=∠ACB.
求证:AB=AB′.
∵CA⊥BB′,∴∠1=∠2=90°.在△ACB和△ACB′中,∠1=∠2,AC=AC,∠ACB= ∠ACB′,∴△ACB≌△ACB′,∴AB=AB′.故测得AB′的长度就是AB的长度.
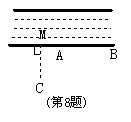
8.解:如答图所示,这样的根据是“垂线段最短”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com