
1、这是本人在我校举行的校长高级研讨班上上的一节展示课。
教材P.178.练习1、2、3;教材P.187中6、7
本节课复习了圆的周长和弧长公式,并在做题中综合复习了正多边形、垂经定理、两圆公切线等有关知识,学习了从实际问题中抽象出数学模型的方法.
1.(复习提问)哪位同学回答圆的周长公式?(安排中下生回答:C=2πR),2.如果⊙O的周长为C,它的半径R,设这个圆的半径增加a,那么它的周长增加多少?(在学生思考、计算后,安排中等生回答:2π
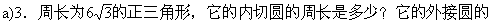
周长是多少?(在学生思考,计算后,安排中下生回答:内切圆周长2π,外接圆周长4π).
(幻灯供题):火车机车上的主动轮直径为1.2米,主动轮每分转400转,火车每小时行几公里(精确到1公里)?
哪位同学知道机车轮子转一圈,在轨道上走多远距离?(安排中上学生回答:1.2π米)你计算的依据是什么?(轮子转一圈,在轨道上的距离就是圆的一个周长.)
请同学们计算出这题的结果(约90公里).
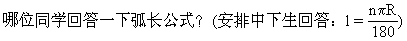
弧长公式中的n与中心角度数n°有什么联系和区别?(安排中上生回答:公式中的n表示1°弧长的n倍,它在数值上恰等于中心角的度数的数值.)
如果已知条件中中心角的度数不仅有度还有分,还有秒,要计算此角所对弧长应首先做什么工作,(安排中等生回答:将度、分、秒转化为度,从而得到公式中所需的n)
同学们请计算这样一道题:在半径10cm的⊙O中,圆心角为32°

幻灯供题:如图7-158,有一圆弧形桥拱,拱的跨度AB=40m,拱形的半径R=29m,求拱形的高和拱形的弧长(保留4个有效数字.)
哪位同学知道,“有一圆弧形桥拱”这句话给我们解题提供什么信息?(找中上生回答,桥拱的弧是一个圆的一部分.)
“拱上跨度AB=40m”又为我们提供什么信息?(安排中上生回答:AB是桥拱弧所在圆的弦,其长40m).
“拱形的半径R=29m”又为我们提供什么信息?(安排中下生回答:桥拱弧所在圆的半径29m)
哪位同学能画出解决此实际问题的几何图形?(安排一名上等生上黑板画,其余学生在练习本上画)
在这个图形中,拱形的高是哪条线段.为什么是它?(安排中上生回答:CD,概括弓形高的定义.)看到这个图,你想到了什么定理?(安排中等生回答:垂经定理.)哪位同学能叙述一下垂径定理?(安排中等生回答)请同学们研究一下拱高怎么求?(安排中下生回答:先用勾股定理求出OD,然后用半径减OD即可).
要求拱形弧长,半径已知,还缺少什么条件?(安排中下生回答,少弧所对中心角的度数)
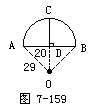
中心角∠AOB的度数你打算通过什么方法求出来?(中图7-159上生回答:作直角三角形AOD).
请同学们完成这题,(安排上等生上黑板)
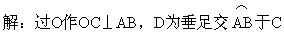
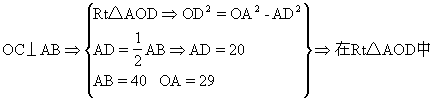
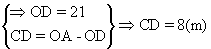
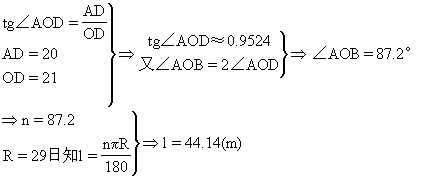
答:拱形的高8m,拱形弧的长约44.14m.
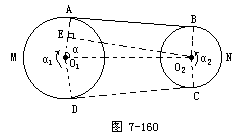
幻灯供题:如图7-160,两个皮带轮的中心的距离为2.1m,直径分别为0.65m和0.24m.(1)求皮带长(保留三个有效数字);(2)如果小轮每分转750转,求大轮每分约转多少转.
“两个皮带轮的中心的距离为2.1m”,给我们解决此题提供了什么数学信息?(安排中等生回答:两个圆的圆心距为2.1m)
题目中皮带长,在图形中指的是哪几部分的和?(安排中等生回答: 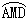 +DC+
+DC+ 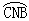 +AB)
+AB)
AB、CD与⊙O1、⊙O2具有什么位置关系?AB与CD具有什么数量关系?根据是什么?(安排中下生回答:AB与CD是⊙O1与⊙O2的公切线,AB=CD,根据的是两圆外公切线长相等.)
前面单元大家已学过了公切线长的求法,哪位同学还记得计算两圆外公切线长的途经?(安排中上学生回答:构造由圆心距、半径差和切线长的平移线段组成的直角三角形,解这个三角形即可)
请同学们把切线长AB求出来,(安排一名中上生到黑板做)
解:(1)作过切点的半径O1A、O1D、O2B、O2C,作O2E⊥O1A,垂足为E
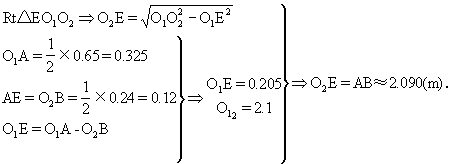
要求
 的长度,已具备了什么条件,还缺少什么条件?(安排中下生:已具备了半径0.325,缺少
的长度,已具备了什么条件,还缺少什么条件?(安排中下生:已具备了半径0.325,缺少  所对圆心角的度数),观察图形,你打算通过什么途径求出
所对圆心角的度数),观察图形,你打算通过什么途径求出
 所对圆心角α1?(安排中上生:α1=360°-2α,而α可通过解Rt△O1EO2解决).
所对圆心角α1?(安排中上生:α1=360°-2α,而α可通过解Rt△O1EO2解决).
请同学们求出
 的长度.(安排一名中上生到黑板前完成此题)
的长度.(安排一名中上生到黑板前完成此题)
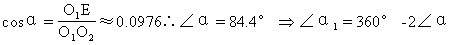
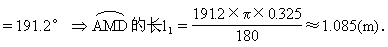
同样要求
 的长度,半经0.12,∠BO2C怎么求?请同学们观察图形,哪位同学谈谈看法:(安排上等生回答:∠BO2C=2∠α=168.8°,因O1A∥O2B,O1D∥O2C所以∠BO2C=2∠α)
的长度,半经0.12,∠BO2C怎么求?请同学们观察图形,哪位同学谈谈看法:(安排上等生回答:∠BO2C=2∠α=168.8°,因O1A∥O2B,O1D∥O2C所以∠BO2C=2∠α)
请同学们求出
 的长度,(安排一名中上生到黑板完成)
的长度,(安排一名中上生到黑板完成)
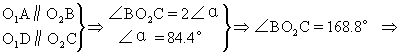
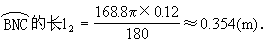
∴皮带长l=l1+l2+2AB=5.62(m).
现在我们解决第(2)个问号,大轮与小轮的半径不同,转数不同,由于皮带传动的作用,大轮与小轮具备一个什么等量关系?(安排中上学生回答:小轮与大轮每分钟所走的路程相等)
如果设大轮每分钟转数为n,哪位同学能列出方程?(安排中等生回答,0.65·π·n=0.24·π×750)
请同学们计算出n来.(安排一中下生报答案:n≈277(转))
上节课我们复习了圆的周长公式,学习了弧长公式,我们说圆的周长公式与弧长公式应用很广泛,并且跟其它知识联系很密切,今天我们继续学习“7.19圆周长、弧长”继续研究它的应用.
由于圆的周长和弧长公式有广泛的应用性,所以在解决实际应用问题中不仅复习了这两个公式而且学会了从中抽象数学模型的方法.由于这两个公式跟其它知识有密切的联系,所以在解决实际问题中又复习了一系列的相关知识,而且又培养了学生综合分析问题解决问题的能力.
5. 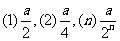 。
。
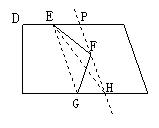
4.方案为:如答图所示,连结EG,过F作PH∥EG,交DC于P,交AB于H, 则EH( 或PG)为新水渠.理由如下:在平行线EG与PH之间,距离处处相等,因此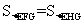 ,故此设计符合题意.
,故此设计符合题意.
3.△MEF是等腰直角三角形.
证明:连结AM,∵M是BC的中点,∠BAC=90°,AB=AC,
∴AM=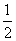 BC= BM,AM平分∠BAC,∴∠MAC=∠MAB=
BC= BM,AM平分∠BAC,∴∠MAC=∠MAB=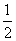 ∠BAC=45°.
∠BAC=45°.
∵AB⊥AC,DE⊥AC,DF⊥AB,∴DE ∥AB,DF∥AC.
∵∠BAC=90°,∴四边形DFAE为矩形,∴DF=AE.
∵DF⊥BF,∠B=45 °, ∴∠BDF=∠B=45°,∴BF=FD,∴AE=BF,
∴△AEM≌△BFM,∴EM=FM,∠AME=∠BMF.
∵∠BMF+∠AMF=90°,∴∠AME+∠AMF=∠EMF=90°,∴△EMF是等腰直角三角形.
2.解:延长BD交AC于E,假设合格,则有∠BDC=∠C+∠CED,∠CED= ∠A+∠B.
∵∠A=90°,∠B=30°,∠C=21°,
∴∠BDC=90°+30°+21°=141°≠148°,
故零件不合格.
1.解:底端水平滑动2m,理由如下:如答图所示,梯子AB=A′B′=10m, 高AC=8m,
∵BC=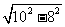 = 6(m),又A′C=6m,∴B′C=
= 6(m),又A′C=6m,∴B′C= = 8(m),
= 8(m),
∴BB′=B′C-BC=8-6=2(m),即梯子底端水平滑动2m.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com