
在小学,同学们除了学习圆柱之外还学习了一个几何体--圆锥,在生活中我们也常常遇到圆锥形的物体,涉及到这些物体表面积的计算.这些圆锥形物体的表面积是怎样计算出来的?这就是本节课“7.21圆锥的侧面展开图”所要研究的内容.
和圆柱一样,圆锥也是日常生活或实践活动中常见物体,在学生学过圆柱的有关计算后,进一步学习圆锥的有关计算,不仅对培养学生的空间观念有好处,而且能使学生体会到用平面几何知识可以解决立体图形的计算,为学习立体几何打基础.
圆锥的侧面展开图不仅用于圆锥表面积的计算,而且在生产中常用于画图下料上,因此圆锥侧面展开图是本课的重点.
本课首先在小学已具有圆锥直观感知的基础上,用直角三角形旋转运动的观点给出圆锥的一系列概念,然后利用圆锥的模型,把其侧面展开,使学生认识到圆锥的侧面展开图是一个扇形,并能将圆锥的有关元素与展开图扇形的有关元素进行相互间的转化,最后应用圆锥及其侧面展开图之间对应关系进行计算.
教材P.183练习1、2;P.188中12.
哪位同学能为本节课作总结?(安排中上学生回答:1.弓形面积的计算:首先看弓形弧是半圆、优弧还是劣弧,从而选择分解方案.2.应用弓形面积解决实际问题.3.分解简单组合图形为规则圆形的和与差.)
(复习提问):1.请回答圆的面积公式.2.请回答扇形的面积公

(以上三问应安排中下生回答)4.请同学看图7-163,弦AB把圆分成两部分,这两部分都是弓形,哪位同学记得弓形的定义?(安排中下生回答:由弦及其所对的弧组成的图形叫做弓形.)
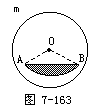

所组的弓形.它的面积能不能跟扇形面积联系上呢?(安排中上生回答:能,连结OA、OB).大家再观察图形,这个弓形的面积如何通过扇形

也就是说组成弓形的弧如果是劣弧,那么它的面积应该等于以此劣弧与半径组成的扇形面积减去这两半径与弦组成的三角形的面积.



和半径OA、OB组成的图形是扇形吗?为什么?(安排中上生回答:是,因为它符合扇形的定义.)
如果弦AB是⊙O的直径,那么以AB为弦,半圆为弧的弓形的面积又是多少?(安排中下生回答:圆面积的一半.)
于是我们得出结论:如果组成弓形的弧是半圆,则此弓形面积是圆面积的一半;如果组成弓形的弧是劣弧则它的面积等于以此劣弧为弧的扇形面积减去三角形的面积;如果组成弓形的弧是优弧,则它的面积等于以此优弧为弧的扇形面积加上三角形的面积.也就是说:要计算弓形的面积,首先观察它的弧属于半圆?劣弧?优弧?只有对它分解正确才能保证计算结果的正确.
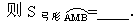

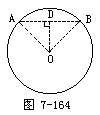
哪位同学知道要对这种题进行计算,首先要作什么工作?(安排中下


三角形AOB的面积怎么求?(安排中上生回答:过O作OD⊥AB,垂

以只要解此△AOD即可求出OD、AD的长,则S△AOB可求.)
请同学们把这题计算出来.(安排一学生上黑板做,其余在练习本上
请同学们讨论研究第2题,并计算出它的结果.(安排中上生上黑板
(幻灯提供例题:)水平放着的圆柱形排水管的截面半径是0.6m,其中水面高是0.3m.求截面上有水的弓形的面积.(精确到0.01m2)
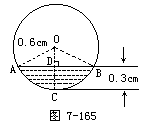
“水平放着的圆柱形排水管的截面半径是0.6m”为你提供了什么数学信息?(安排中上生回答:⊙O的半径是0.6m.)“其中水面高是0.3m”.又为你提供了什么信息?(安排中上生回答:弓形高CD是0.3m.)“求截面上有水的弓形的面积为你提供什么信息?(安排中等生回答:
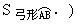
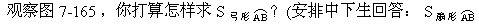

长,看看已知条件,你打算怎么办?(安排中上学生回答:因弓形高CD已知,半径已知,所以弦心距OD可求,根据垂径定理,Rt△AOD可解,即∠AOD的度数可求,所以∠AOB的度数可求.n既然可求当然
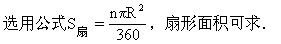
请问△AOB的面积又该如何求?(安排中等学生回答:通过解此△AOD可求出AD的长,再据垂径定理可求AB的长,OD已求,所以S△AOB可求.)
请同学们完成这道应用题.(安排一位中上学生到黑板做,其余学生在练习本上完成).
弓形面积虽然没有计算公式,但可以选用图形分解法,将它转化为扇形与三角形的和或差来解决,那么其它一些组合图形,不也可以用图形分解法来求其面积吗?
幻灯示题:如图7-166,已知正△ABC的边长为a,分别以A、B、
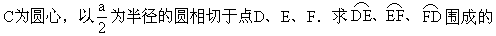
图形面积S.
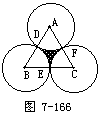
显然图形中阴影部分的面积无计算公式,因此必须将它转化为有公式图形的和或差来解决.想想看,你打算如何求S阴?(安排中等生回答:S阴=S正△ABC-3S扇)
正三角形的边长为a,显然S正△ABC可求.由于正△ABC,所以∠
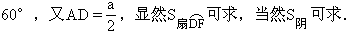
请同学们完成此题.(安排一中上学生上黑板,其余在练习本上完成).
幻灯示题:已知:⊙O的半径为R,直径AB⊥CD,以B为圆心,

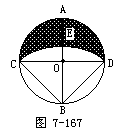
大家观察,图(7-167)中的阴影部分面积应当如何求?(安排中下生回
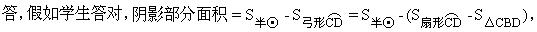

我的看法对还是不对?为什么?(安排举手的学生回答:图形BCAD不是扇形,因为扇形的定义是在同一个圆中,一条弧和过弧端点的两条半径
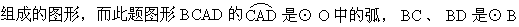
的半径.因此将阴影面积看成两扇形的差是错误的.)
请同学们按照正确思路完成此题.(安排一中等学生上黑板,其余学生在练习本上做)
上一节我们复习了圆的面积,在它的基础上我们学习了扇形的面积,本节课就要在前一课的基础上学习弓形面积的计算.
弓形是一个最简单的组合图形之一,由于有圆的面积、扇形面积、三角形面积做基础,很容易计算弓形的面积.
由于计算弓形的面积不像圆面积和扇形面积那样有公式,当弓形的弧小于半圆时,弓形的面积等于扇形面积与三角形面积的差;当弓形的弧大于半圆时,它的面积等于扇形面积与三角的面积的和;当弓形弧是半圆时,它的面积是圆面积的一半.也就是说要计算弓形的面积首先要观察这个弓形是怎么组合而成的,从而得到启发;一些组合图形的面积总要分解为几个规则图形的和与差来解决的方法.所谓规则图形指的是有计算公式的图形.因此弓形面积的计算以及受它启发的分解组合图形求面积的方法就是本节课的重点.本节拟就三部分组成:1.师生共同观察分解弓形,然后作有关的练习.2.运用弓形面积的计算解决实际问题.3.受分解弓形的启发分解一些简单的图形.
15.(12分)如图,某工厂要选一块矩形铁皮加工成一个底面半径为20cm,高为40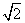 cm的锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少cm的矩形铁皮,才能使用料最省?
cm的锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少cm的矩形铁皮,才能使用料最省?
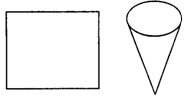
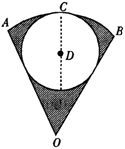
14.(12分)如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,求:
(1)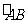 的长;(2)阴影部分面积.
的长;(2)阴影部分面积.
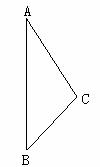
13.(12分)在△ABC中,∠A=30°,AC=8,BC=5,以直线AB为轴,将△ABC旋转一周得到一个旋转体,求这个旋转体的全面积.
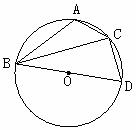
12.(12分)如图,△ABC内接于⊙O,BD是⊙O的直径,∠A=120°,CD=2cm,求扇形BOC的面积.
11.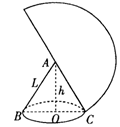 (12分)如图,一个圆锥的高为3
(12分)如图,一个圆锥的高为3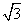 cm,侧面展开图是半圆,求:
cm,侧面展开图是半圆,求:
(1)圆锥的母线与底面半径之比;(2)锥角的大小;(3)圆锥的表面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com