
4、已知正三角形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
思考应用
问题:正方形的边长为4,以各边为直径,在正方形内画半圆,求所围成的图形(阴影部分)的面积.
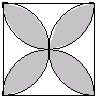
反思:①对图形的分解不同,解题的难易程度不同,解题中要认真观察图形,追求最美的解法;②图形的美也存在着内在的规律.(3)求面积问题的常用方法有:直接公式法,和差法,割补法等.
作业与练习、
3、已知扇形的半径为5cm,面积为20 cm2,则扇形弧长为______cm.
2、已知扇形的圆心角为210°,弧长是28π,则扇形的面积为______.
1、扇形的面积为 cm2,扇形所在圆的半径 cm,则圆心角为______度.
4、通过弧长公式、扇形面积公式的推导,培养学生抽象、理解、概括、归纳能力和迁移能力
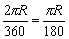 教学过程(一)
教学过程(一)
1°圆心角所对弧长= ;
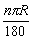 n°圆心角所对的弧长是1°圆心角所对的弧长的n倍;
n°圆心角所对的弧长是1°圆心角所对的弧长的n倍;
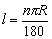 n°圆心角所对弧长 = .
n°圆心角所对弧长 = .
归纳结论:若设⊙O半径为R, n°圆心角所对弧长l,则 (弧长公式)
例1、填空:
(1)半径为3cm,120°的圆心角所对的弧长是_______cm;
(2)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______;
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______.
(在弧长公式中l、n、R知二求一.)
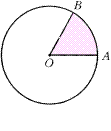 例2、 如图,圆心角为60°的扇形的半径为10厘米,求这个扇形周长
例2、 如图,圆心角为60°的扇形的半径为10厘米,求这个扇形周长
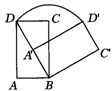
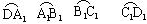 例3、如图:四边形ABCD是正方形,曲线DAlBlClDl……叫做“正方形的渐开线”,其中中 、 、 、 … 的圆心依次按A、B、C、D循环,它们依次连接.取AB=l,则
例3、如图:四边形ABCD是正方形,曲线DAlBlClDl……叫做“正方形的渐开线”,其中中 、 、 、 … 的圆心依次按A、B、C、D循环,它们依次连接.取AB=l,则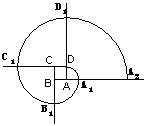 曲线DAlBl…C2D2的长是______(结果保留π).
曲线DAlBl…C2D2的长是______(结果保留π).
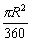 (二)扇形的面积
(二)扇形的面积
(1)圆面积S=πR2;(2)圆心角为1°的扇形的面积= ;
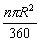 (3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
(4)圆心角为n°的扇形的面积 = .
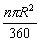 归纳结论:若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
归纳结论:若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
S扇形= (扇形面积公式)
 提出问题:扇形的面积公式与弧长公式有联系吗?(教师组织学生探讨)
提出问题:扇形的面积公式与弧长公式有联系吗?(教师组织学生探讨)
S扇形= lR
想一想:这个公式与什么公式类似?(教师引导学生进行,或小组协作研究)
与三角形的面积公式类似,只要把扇形看成一个曲边三角形,把弧长l看作底,R看作高就行了.这样对比,帮助学生记忆公式.实际上,把扇形的弧分得越来越小,作经过各分点的半径,并顺次连结各分点,得到越来越多的小三角形,那么扇形的面积就是这些小三角形面积和的极限.要让学生在理解的基础上记住公式.
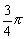 例题与练习:
例题与练习:
3、掌握扇形面积公式的推导过程,运用扇形面积公式进行一些有关计算;
1.掌握弧长的计算公式;
2能灵活应用弧长的计算公式解决有关的问题,并在应用中培养学生的分析问题、解决问题的能力;
3.如图所示,在计算机白色屏幕上,有一矩形着色画刷ABCD,AB=1,AD=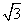 ,将画刷以B为中心,按顺时针转动A′B′C′D′位置(A′点转在对角线BD上),求屏幕被着色的面积.
,将画刷以B为中心,按顺时针转动A′B′C′D′位置(A′点转在对角线BD上),求屏幕被着色的面积.
2.如图,若⊙O的周长为20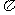 cm,⊙A、⊙B的周长都是4
cm,⊙A、⊙B的周长都是4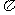 cm,⊙A在⊙O内沿⊙O滚动,⊙B在⊙O外沿⊙O滚动,⊙B转动6周回到原来的位置,而⊙A只需转动4周即可,你能说出其中的道理吗?
cm,⊙A在⊙O内沿⊙O滚动,⊙B在⊙O外沿⊙O滚动,⊙B转动6周回到原来的位置,而⊙A只需转动4周即可,你能说出其中的道理吗?

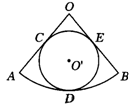
1.已知如图所示,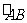 所在圆的半径为R,
所在圆的半径为R,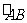 的长为
的长为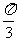 R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com