
6.有两组扑克牌各三张,牌面数字分别为1、2、3,随意从每组中牌中各抽取一张,数字和是奇数的概率是( ).
A. B.
B. C.
C. D.
D.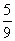
5.在中考体育达标跳绳项目测试中,1分钟跳160次为达标。小敏记录了他预测时1分钟跳的次数分别为145、155、140、162、164,则他在该次预测中达标的概率是( ).
A. 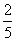 B.
B.  C.
C. 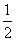 D. 1
D. 1
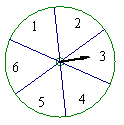
4.下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.其中,你认为正确的见解有( )
A.1个 B.2个 C.3个 D.4个
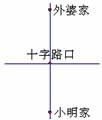
3.如图,小明周末到外婆家,走到十字路口处,记不清前面哪条路通往外婆家,那么他能一次选对路的概率是( ).
 A.
A.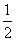 B.
B.  C.
C. 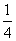 D.
0
D.
0
2. 下列说法:(1)不可能发生和必然发生的都是确定的;(2)可能性很大的事情是必然发生的;(3)不可能发生的事情包括几乎不可能发生的事情;(4)冬天里武汉一定会下雪.其中,正确的个数为( ).
下列说法:(1)不可能发生和必然发生的都是确定的;(2)可能性很大的事情是必然发生的;(3)不可能发生的事情包括几乎不可能发生的事情;(4)冬天里武汉一定会下雪.其中,正确的个数为( ).
A. 1个 B. 2个 C. 3个 D. 4个
1.下列事件中是随机事件有( )个.
(1)在标准大气压下水在0℃时开始结成冰;
(2)掷一枚六个面分别标有l-6的数字的均匀骰子,骰子停止转动后偶数点朝上;
(3)从一副扑克牌中任意抽出一张牌,花色是红桃;
(4)打开电视机,正在转播足球比赛;
(5)小麦的亩产量为1000公斤.
A. 1个 B.2个 C.3个 D.4个
24.4.1 弧长和扇形面积

|
教 学 目 标 |
知识技能 |
掌握弧长和扇形面积公式的推导过程,初步运用扇形面积公式进行一些有关计算. |
|
数学思考 |
通过弧长和扇形面积公式的推导过程,发展学生分析问题、解决问题的能力. |
|
|
解决问题 |
通过扇形面积公式的推导,发展学生抽象、理解、概括、归纳能力和迁移能力. |
|
|
情感态度 |
在扇形面积公式的推导和例题教学过程中,渗透“从特殊到一般,再由一般到特殊”的辩证思想. |
|
|
重点 |
弧长,扇形面积公式的导出及应用. |
|
|
难点 |
对图形的分析 |

|
24.4 弧长和扇形面积公式 弧长公式: 例题分析 扇形面积公式: |


|
问题与情境 |
师生行为 |
设计意图 |
活动一:创设情境,引入课题 制造弯形管道时,经常要先按中心线计算“展直长度”(图1中虚线的长度),再下料,这就涉及到计算弧长的问题. 制造弯形管道时,经常要先按中心线计算“展直长度”(图1中虚线的长度),再下料,这就涉及到计算弧长的问题.活动二:思考:试一试 问题1:你还记得圆周长的计算公式吗?圆的周长可以看作多少度的圆心角所对的弧长?由此出发,1°的圆心角所对的弧长是多少?  的圆心角呢? 的圆心角呢?设:圆的半径为  ,求 ,求 的圆心角所对的弧长. 的圆心角所对的弧长.问题2:你还记得圆面积的计算公式吗?圆面积可以看作多少度的圆心角所对的扇形的面积?1°的圆心角所对的扇形面积是多少?  的圆心角呢? 的圆心角呢?设:已知⊙O半径为  ,求 ,求 的圆 的圆心角所对的扇形面积. |
教师提出问题后,学生认真思考,说明解题的关键是求中心线“展直长度”,但如何求呢?从而引出今天的课题:弧长和扇形面积. 教师根据学生已有的知识结构,强调弧、扇形的有关概念. 教师引导学生由圆周长入手,推导弧长公式. 教师提出问题 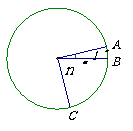 后,学生认真思考,由中等学生回答:圆周长为 后,学生认真思考,由中等学生回答:圆周长为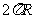 ,可看作是360°的圆心角所对的弧长;1°的圆心角所对的弧长为 ,可看作是360°的圆心角所对的弧长;1°的圆心角所对的弧长为 ;圆心角为n°的弧长是圆心角为1°的弧长的n倍;∴ ;圆心角为n°的弧长是圆心角为1°的弧长的n倍;∴ 的圆心角所对的弧长为 的圆心角所对的弧长为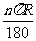 . .∴弧长公式为: 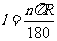 注:不写度,  和180表示的是倍、分关系. 和180表示的是倍、分关系.教师关注学生对公式的理解程度. 教师引导学生类比弧长公式的推导过程,推导出扇形面积公式: (1)圆面积S=πR2,可以看作是360°的圆心角所对的扇形面积; |
由实际问题引出课题,可激发学生的学习兴趣. 在教师的引导下,推出弧长公式,使学生明确公式的推导过程,知道公式的来龙去脉,更要学会学习新知识的方法. 教会学生用类比的方法研究问题. |

|
问题与情境 |
师生行为 |
设计意图 |
|
比较扇形面积公式和弧长公式,看看它们之间有什么关系? 活动三:解决问题 对于本节开头提出的问题,你能解答吗? 活动四:比一比,看谁算得快? 练习: 1.半径为4,80°的圆心角所对的弧长为 ; 2.扇形的弧长为 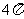 ,半径为3,则其面积为 ; ,半径为3,则其面积为 ;3.扇形的半径为24,面积为240 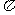 ,则这个扇形的圆心角为 ; ,则这个扇形的圆心角为 ;活动五:例题分析 如图2,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(精确到0.012m) |
(2)圆心角为1°的扇形的面积=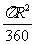 . .(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍; ∴扇形面积公式为 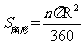 . .经过观察,学生能够看出: 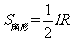 ,其中, ,其中, 是扇形的弧长, 是扇形的弧长, 为半径. 为半径.学生观察本节开头提出的问题,根据图1中所给的数据,由弧长公式,就可以得出  的长: 的长: 因此所要求的展直长度 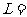 2×700+1570=2970 2×700+1570=2970∴所要求的展直长度约为2970mm. 教师提出问题后,学生认真思考,独立完成,看谁最先做好. 教师出示例题后,引导学生分析已知条件,教师要关注学生对题目中的有关概念是否清楚,如水面高指的是什么? |
类比的推出扇形面积公式,并由学生比较两个公式的联系,使学生在学习知识时,明确知识之间的联系,在解题时,根据题目条件,选择适当的公式. 数学知识来源于生活实际,又用来解决实际中的问题,强化数学的应用意识. 迅速、正确的运用所学公式解题,培养学生良好的学习习惯,训练学生的解题速度. 培养学生综合运用知识解题的能力. |


|
问题与情境 |
师生行为 |
设计意图 |
 活动六:理一理 学生小结 教师归纳 布置作业: A组: P122页练习:1,2, P124页习题24.4:1.(1)、(2),2,6,7. B组: P122页练习:1,2, P124页习题24.4:2,3,5,6. |
经过分析,学生知道了水面高即弧 的中点到弦AB的距离. 的中点到弦AB的距离.因此想到做辅助线的方法: 连接OA、AB,过O作OC⊥AB于点D,交  于点C. 于点C.教师关注学生对题目的理解,师生共同分析题目条件后,由学生独立写出解题过程,用实物投影展示学生的解题过程,再由学生对解题过程给予评价. 由学生谈谈本节课学习的体会和收获,各抒己见.教师对学生的回答给予帮助,让语言表达更准确. 知识:弧长公式 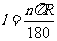 ; ;扇形面积公式: 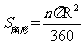  . .能力:灵活运用公式解决实际问题. 数学思想:数形结合思想. 学生课下独立完成. 教师对学生的作业在批改后及时反馈. B组补充作业:  已知:如图,矩形ABCD中,AB=1cm,BC=2cm,以B为圆心,BC为半径作 已知:如图,矩形ABCD中,AB=1cm,BC=2cm,以B为圆心,BC为半径作 圆弧交AD于F,交BA延长线于E,求扇形BCE被矩形所截剩余部分的面积. 圆弧交AD于F,交BA延长线于E,求扇形BCE被矩形所截剩余部分的面积. |
学生在学习新知识的同时要想到学过的知识,在这里就运用了垂径定理. 巩固所学知识,达到复习的目的,教师及时了解学生对本节知识的掌握情况,对教学进度和方法进行适当调整,并对有困难的学生给予指导。 发展学生的解决实际问题的能力和应用意识.初步探索建立数学模型.让学生畅所欲言,教师了解学生的学习情况,并让学生逐渐的学会总结。 检查知识的落实性,以便发现问题和及时解决问题。 继续培养学生的探究意识和学习上持之以恒的精神. |
4.探究活动: 已知由若干根钢管的外直径均为d,想用一根金属带紧密地捆在一起,求金属带的长度.
请根据下列特殊情况,找出规律,并加以证明.
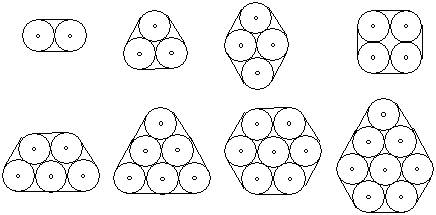
提示:设钢管的根数为n,金属带的长度为Ln如图:
当n=2时,L2=(π+2)d. 当n=3时,L3=(π+3)d. 当n=4时,L4=(π+4)d.
当n=5时,L5=(π+5)d. 当n=6时,L6=(π+6)d. 当n=7时,L7=(π+6)d.
当n=8时,L8=(π+7)d.
猜测:若最外层有n根钢管,两两相邻接排列成一个向外凸的圈,相邻两圆是切,则金属带的长度为L=(π+n)d.
课堂总结: 这节课学习了哪些计算公式? 你能灵活应用弧长与扇形的计算公式解决有关的问题吗?
更多精品资源欢迎您
点击“K12个人专辑:吴晓刚”
http://derup/page/user_mode.php/wxstrong

2、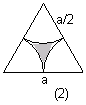 如图2所示,边长为a的正三角形中,阴影部分的面积为______.
如图2所示,边长为a的正三角形中,阴影部分的面积为______.
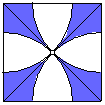
3如图,在边长l的正方形中,以各顶点为圆心,
对角线长的一半为半径在正方形内画弧,
则图中阴影部分的面积为_______.
1、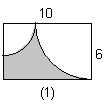 如图1所示,矩形中长和宽分别为10 cm和6cm,则阴影部分的面积为______.
如图1所示,矩形中长和宽分别为10 cm和6cm,则阴影部分的面积为______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com